Нормальное уравнение прямой можно получить из общего уравнения прямой. Если прямая на плоскости задана иным уравнением прямой, то это уравнение следует сначала привести к общему уравнению прямой, а уже после этого приводить общее уравнение прямой к нормальному виду.
Итак, покажем приведение общего уравнения прямой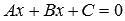 
к нормальному уравнению прямой.
Чтобы привести общее уравнение прямой к нормальному виду нужно обе части равенства 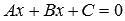умножить на так называемый нормирующий множитель, который равен 
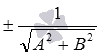. Знак нормирующего множителя берется противоположным знаку слагаемого С. Если C = 0, то знак нормирующего множителя не имеет значения и может быть выбран произвольно.
Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой.
Обозначим расстояние от точки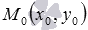 
до прямой, заданной нормальным уравнением 
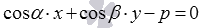, буквой 
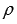. Тогда расстояние 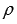может быть вычислено по формуле 
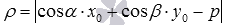. То есть, для нахождения расстояния от точки до прямой следует подставить координаты заданной точки в левую часть нормального уравнения заданной прямой и взять абсолютную величину полученного значения.
