Скалярным произведением двух векторов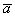 
и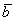 
называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними: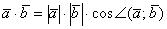
Вот это вот уже вполне строгое определение.
Акцентируем внимание на существенной информации:
Обозначение: скалярное произведение обозначается через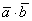 
или просто 
.
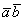Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись: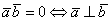 
Скалярное произведение положительное, если угол между векторами острый
Скалярное произведение отрицательное, если угол между векторами тупой.
Для произвольных векторов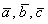 
и любого числа 
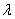справедливы следующие свойства:
1) 
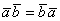– переместительный или коммутативный закон скалярного произведения.
2) 
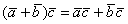– распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
3) 
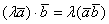– сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
