2 вектора плоскости линейно независимы в том и только том случае, если они не коллинеарны.
Базисом плоскости называется пара линейно независимых векторов, вязтых в определенном порядке, при этом любой вектор плоскости является линейной комбинацией базисных векторов*.
Линейная комбинация - разложение вектора v по базису (e1, e2). Расскладывается следующим образом: альфа*е1 + бетта*е2. Числа 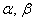 называют координатами вектора в данном базисе.
называют координатами вектора в данном базисе.

