Правило сложения векторов по правилу треугольников
Рассмотрим два произвольных ненулевых вектора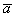 
и 
:
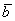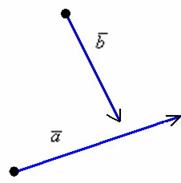
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор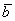 
от конца вектора 
:
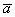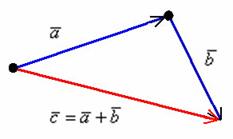
Суммой векторов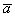 
и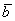 
является вектор 
.
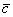Кстати, если вектор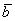 
отложить от начала вектора 
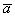, то получится эквивалентное правило параллелограмма сложения векторов.
Умножение вектора на число
Произведением ненулевого вектора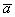 
на число 
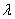является такой вектор 
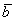, длина которого равна 
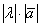, причём векторы 
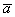и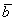 
сонаправлены при 
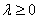и противоположно направлены при 
.
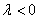Разбираемся более детально:
1) Направление. Если множитель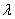 
отрицательный, то вектор меняет направление на противоположное.
2) Длина. Если множитель заключен в пределах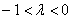 
или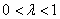 
, то длина векторауменьшается. Так, длина вектора 
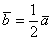в два раза меньше длины вектора 
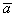. Если множитель 
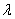по модулю больше единицы, то длина вектора увеличивается в 
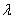раз.
3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,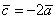 
. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны. Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.
