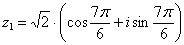Уравнение вида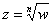 
имеет ровно 
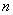корней 
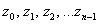, которые можно найти по формуле:
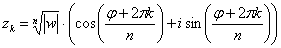, где 
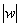– это модуль комплексного числа 
, 
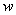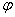– его аргумент, а параметр 
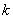принимает значения: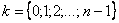 
ПРИМЕР
Найти корни уравнения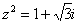 
Перепишем уравнение в виде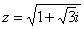 
В данном примере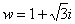 
, 
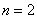, поэтому уравнение будет иметь два корня: 
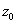и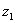 
.
Общую формулу можно сразу немножко детализировать: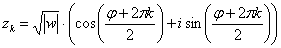
, 
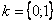
Теперь нужно найти модуль и аргумент комплексного числа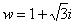 
:
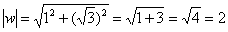
Число 
располагается в первой четверти, поэтому: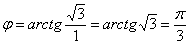
Напоминаю, что при нахождении тригонометрической формы комплексного числа всегда желательно сделать чертеж.
Еще более детализируем формулу: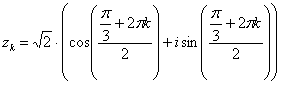
, 
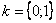
На чистовик так подробно оформлять, конечно, не нужно, это сделано мной для того, чтобы вам было понятно, откуда что взялось.
Подставляя в формулу значение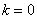 
, получаем первый корень: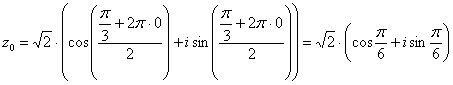
Подставляя в формулу значение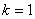 
, получаем второй корень: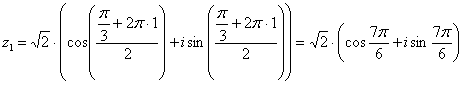
Ответ: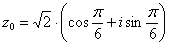 
, 
