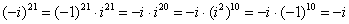Если комплексное число представлено в тригонометрической форме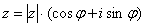 
, то при его возведении в натуральную степень 
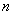справедлива формула:
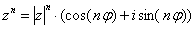
Данная формула следует из правила умножения комплексных чисел, представленных в тригонометрической форме: чтобы найти произведение чисел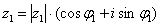 
, 
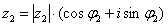нужно перемножить их модули и сложить аргументы: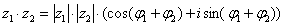
Аналогично для показательной формы: если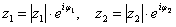 
, то: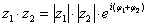
Если мнимая единица возводится в четную степень, то техника решения такова: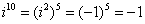
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень: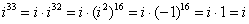
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:
