Тригонометрическая форма
Если вещественную 
и мнимую 
части комплексного числа выразить через модуль 
и аргумент 
(
, 
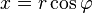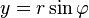), то всякое комплексное число
, кроме нуля, можно записать в тригонометрической форме
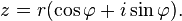
Показательная форма
Применяя формулу Эйлера к тригонометрической форме, получим показательную форму комплексного числа:
где 
— расширение экспоненты для случая комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:
