Понятие комплексного числа и операции над ними. Алгебраическая форма записи.

Ко́мпле́ксные чи́сла — числа вида $x+iy$ , где $x$ и $y$ — вещественные числа, $i$ — мнимая единица (величина, для которой выполняется равенство: $i^2=-1$ ). Множество всех комплексных чисел с арифметическими операциями является полем и обычно обозначается C

Действия

Сравнение
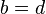$a+bi=c+di$ означает, что $a=c$ и $b=d$ (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение
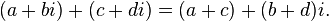
$(a+bi)+(c+di)=(a+c)+(b+d)i.$
Вычитание
$(a+bi)-(c+di)=(a-c)+(b-d)i.$
Умножение
$(a+bi)\cdot(c+di)=ac+bci+adi+bdi^2=(ac-bd)+(bc+ad)i.$
Деление
$\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac+bd}{c^2+d^2}+\left(\frac{bc-ad}{c^2+d^2}\right)i.$
- В частности,
  $\frac{1}{a+bi}=\frac{a}{a^2+b^2}-\left(\frac{b}{a^2+b^2}\right)i.$

Алгебраическая форма

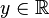Запись комплексного числа $z$ в виде $x+iy$ , где $x$ и $y\in\R$ , называется алгебраической формой комплексного числа.