Вопрос 20. Анализ напряженного состояния балки при поперечном изгибе.

Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты. При изгибе возникают деформация, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса.
Для исследования напряженного состояния в произвольной точке балки, испытывающей поперечный изгиб, выделим из сос­тава балки вокруг исследуемой точки элементарную призму, так чтобы вертикальная площадка явля­лась частью поперечного сечения балки, а наклонная площадка составляла произвольный угол относительно горизонта. Прини­маем, что выделенный элемент имеет следующие размеры по координатным осям: по продольно оси - dz, т.е. по оси z; по вер­тикальной оси - dy, т.е. по оси у; по оси х - равный ширине балки. Обозначим величины нормальных и касательных напряжений на наклонной площадке через     , соответственно. Принимая площадь наклонной площадки dF , для вертикальной и горизон­тальной площадок будем иметь  , соответственно.

Составляя уравнения равновесия для элементарной вырезанной призмы, получим: 

откуда будем иметь: ;

.Следовательно, окончательные выражения напряжений на на­клонной площадке принимают вид:

Определим ориентацию площадки, т.е. значение 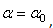, при котором напряжение  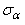 принимает экстремальное значение. Со­гласно правилу определения экстремумов функций из математиче­ского анализа, возьмем производную функции  от alfa  и прирав­няем ее нулю: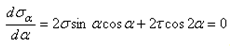.Предполагая  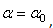 , получим: .

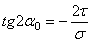Откуда окончательно будем иметь: . Экстремальн. напряжения возникают на двух взаимно перпендикулярных площадках, называ­емых главными, а сами напряжения - главными напряже­ниями. Сопоставляя выражения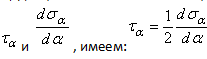  

откуда и следует, что касательные напряжения на главных пло­щадках всегда равны нулю.В заключение, с учетом известных тригонометрических тож­деств:

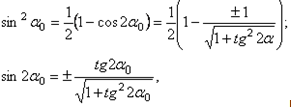 и ,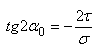

определим гл. напряжения, выражая из