Функция φ(x) называется особым решением дифференциального уравнения F(x,y,y′)=0, если единственность решения нарушается в каждой точке этой функции в области определения дифференциального уравнения. Геометрически это означает, что через каждую соответствующую точку(x0,y0) проходит более одной интегральной кривой с общей касательной.
Примечание: Иногда используется более слабое определение особого решения, когда единственность решения нарушается лишь в некоторых точках.
Особое решение дифференциального уравнения не описывается общим интегралом. Поэтому, оно не выводится из общего решения ни при каком значении постоянной C. Это можно проиллюстрировать следующим примером:
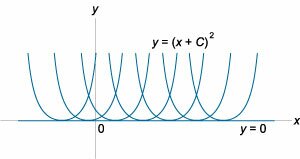
Пусть требуется решить уравнение (y′)2−4y=0. Видно, что общее решение данного уравнения описывается функцией y=(x+C)2. Графически общее решение представляется в виде семейства парабол (Рисунок 1).
 |
|
|
|
Рис.1
|
|
Кроме этого, функция y=0 также удовлетворяет дифференциальному уравнению. Однако эта функция не содержится в общем решении! Поскольку через каждую точку прямой y=0 проходит более одной интегральной кривой, то единственность решения на этой прямой нарушается, и, следовательно, данная прямая является особым решением дифференциального уравнения.
Одним из способов нахождения особого решения является исследование так называемого p-дискриминантадифференциального уравнения. Если функция F(x,y,y′) и ее частные производные ∂F∂y,∂F∂y′ непрерывны в области определения дифференциального уравнения, то особое решение находится из системы уравнений:{F(x,y,y′)=0∂F(x,y,y′)∂y′=0.Уравнение ψ(x,y)=0, которое получается при решении данной системы, называется p-дискриминантомдифференциального уравнения. Соответствующая кривая, определенная этим уравнением, называется p-дискриминантной кривой.

