1.|a| = √ax2 + ay2 + az2
2
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и bпримет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | = | 3 | . |
| 4 | 8 | 12 |
| Вектора a и с не коллинеарны т.к. | 1 | = | 2 | ≠ | 3 | . |
| 5 | 10 | 12 |
| Вектора с и b не коллинеарны т.к. | 5 | = | 10 | ≠ | 12 | . |
| 4 | 8 | 12 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay. Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение na:
na = {2 · 0; 2 · 3; 2 · 1} = {0; 6; 2}Так как b = na, то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Значит:
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
3.
Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Решение:
p · q = (a + 3b) · (5a - 3b) = 5 a · a - 3 a · b + 15 b · a - 9 b · b == 5 |a|2 + 12 a · b - 9 |b|2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ - 9 · 22 = 45 +36 -36 = 45.
Пример вычисления скалярного произведения векторов для пространственных задач
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 - 5 = 15.
Пример вычисления скалярного произведения для n -мерных векторов
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 - 5 -4 = 11.
4.Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 - 2 + 0 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны
5.
Решение:
| a × b = | i | j | k | = |
| 1 | 2 | 3 | ||
| 2 | 1 | -2 |
= i(2 · (-2) - 3 · 1) - j(1 · (-2) - 2 · 3) + k(1 · 1 - 2 · 2) =
= i(-4 - 3) - j(-2 - 6) + k(1 - 4) = -7i + 8j - 3k = {-7; 8; -3}
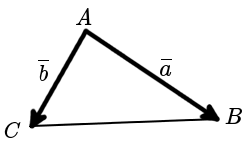
Решение: Найдем векторное произведение этих векторов:
| a × b = | i | j | k | = |
| -1 | 2 | -2 | ||
| 2 | 1 | -1 |
= i(2 · (-1) - (-2) · 1) - j((-1) · (-1) - (-2) · 2) + k((-1) · 1 - 2 · 2) =
= i(-2 + 2) - j(1 + 4) + k(-1 - 4) = -5j - 5k = {0; -5; -5}
Из свойств векторного произведения:
| SΔ = | 1 | |a × b| = | 1 | √02 + 52 + 52 = | 1 | √25 + 25 = | 1 | √50 = | 5√2 |
| 2 | 2 | 2 | 2 | 2 |
Ответ: SΔ = 2.5√2.
6.
Решение:
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2
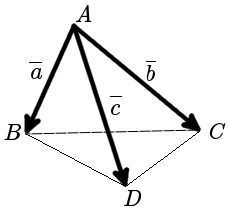
Решение: Найдем смешанное произведение этих векторов:
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | -1 | 1 | ||
| 2 | 0 | -1 |
= 1·(-1)·(-1) + 2·1·2 + 3·1·0 - 3·(-1)·2 - 2·1·(-1) - 1·1·0 =
= 1 + 4 + 0 + 6 + 2 - 0 = 13
Найдем объем пирамиды воспользовавшись свойствами:
| Vпир = | 1 | |a · [b × c]| = | 13 | = 2 | 1 |
| 6 | 6 | 6 |
7. Пример 1. Проверить компланарны ли три вектора a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.
Решение: найдем смешанное произведение векторов
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2
Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.

