Точка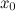 
называется точкой локального максимума функции 
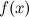, если существует такая окрестность этой точки, что для всех 
из этой окрестности выполняется неравенство: 
.
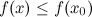Точка 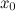называется точкой локального минимума функции 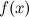, если существует такая окрестность этой точки, что для всех из этой окрестности 
.
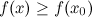Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка 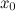называется точкой строгого локального максимума функции 
, если для всех из окрестности этой точки будет справедливо строгое неравенство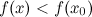
.
Точка 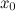называется точкой строгого локального минимума функции , если для всех из окрестности этой точки будет справедливо строгое неравенство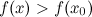
.
Наибольшее или наименьшее значение функции на промежутке называетсяглобальным экстремумом.
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума
(Необходимое условие экстремума)
Если функция имеет экстремум в точке 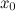, то ее производная 
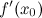либо равна нулю, либо не существует.
Точки, в которых производная равна нулю: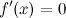 
, называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То естькритические точки - это либо стационарные точки (решения уравнения 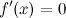), либо это точки, в которых производная 
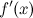не существует.
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
