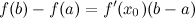Теорема Ферма
Теорема Ферма. (О равенстве нулю производной)
Пусть функция 
удовлетворяет следующим условиям:
- она дифференцируема на интервале
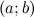; - достигает наибольшего или наименьшего значения в точке
.
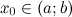Тогда производная в этой точке равна нулю, то есть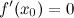 
.
Следствие. (Геометрический смысл теоремы Ферма)
В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.
Теорема Ролля
Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)
Пусть функция
- непрерывна на отрезке
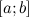; - дифференцируема на интервале ;
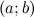- на концах отрезка 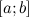принимает равные значения
.
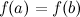Тогда на интервале 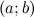найдется, по крайней мере, одна точка 
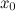, в которой .
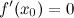Следствие. (Геометрический смысл теоремы Ролля)
Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.
Следствие.
Если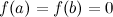 
, то теорему Ролля можно сформулировать следующим образом: между двумя последовательными нулями дифференцируемой функции имеется, хотя бы один, нуль производной.
Теорема Лагранжа
Теорема Лагранжа. (О конечных приращениях)
Пусть функция
- непрерывна на отрезке ;
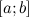- дифференцируема на интервале .
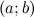Тогда на интервале 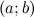найдется по крайней мере одна точка 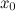, такая, что
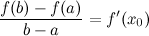
Теорема Ролля есть частный случай теоремы Лагранжа, когда .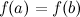
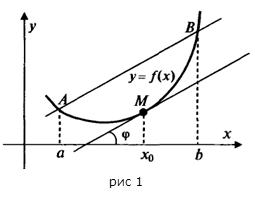
Следствие. (Геометрический смысл теоремы Лагранжа)
На кривой между точками 
и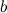 
найдется точка 
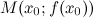, такая, что через эту точку можно провести касательную, параллельную хорде 
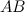(рис. 1).
Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:
