Обратная матрица
На множестве матриц не определена операция деления, она заменена умножением на обратную матрицу.
Замечание Обратная матрица существует только для квадратных матриц с не равными нулю определителями.
Свойства обратной матрицы:
1° 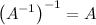
2° 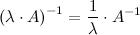
3° 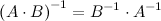
4° 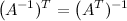
Теорема 4.1. (необходимое и достаточное условие существования обратной матрицы). Обратная матрица A существует тогда и только тогда, когда исходная матрица А невырожденная.
существует тогда и только тогда, когда исходная матрица А невырожденная.
Доказательство. Необходимость. Пусть матрица А имеет обратную A , т. е. A
, т. е. A A
A  AA
AA
 E. По свойству 10 определителей имеем D(A
E. По свойству 10 определителей имеем D(A A)
A)  = D(A
= D(A )D(А)
)D(А)  D(E) = 1 и, следовательно, D(А)
D(E) = 1 и, следовательно, D(А)  0.
0.
Достаточность. Пусть D(А)  0. Рассмотрим квадратную матрицу n-го порядка
0. Рассмотрим квадратную матрицу n-го порядка  , называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы
, называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы  , транспонированной к матрице А:
, транспонированной к матрице А:
 .
.
Легко показать, что
 .
.
Отсюда следует, что если в качестве обратной матрицы взять матрицу A
 , то произведения A
, то произведения A A и AA
A и AA равны единичной матрице E n-го порядка: A
равны единичной матрице E n-го порядка: A A
A AA
AA
 E.
E.
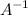 называется обратной к невырожденной матрице
называется обратной к невырожденной матрице  , если
, если 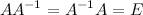 , где
, где 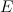 - это единичная матрица соответствующего порядка.
- это единичная матрица соответствующего порядка.

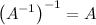
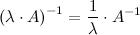
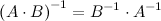
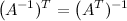
 существует тогда и только тогда, когда исходная матрица А невырожденная.
существует тогда и только тогда, когда исходная матрица А невырожденная. AA
AA 0.
0. , называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы
, называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы  , транспонированной к матрице А:
, транспонированной к матрице А: .
. .
. , то произведения A
, то произведения A