Если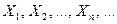 
– попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа 
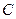), то, как бы мало ни было положительное число 
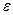, вероятность неравенства
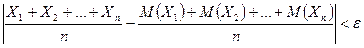
будет как угодно близка к единице, если число случайных величин достаточно велико.
Другими словами, в условиях теоремы
.
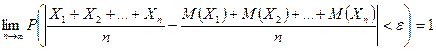Формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. Однако на практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. И если допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева.
Обозначим математическое ожидание каждой из случайных величин через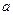 
; в рассматриваемом случае, среднее арифметическое математических ожиданий, как легко видеть, также равно 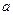. Сформулируем теорему Чебышева для рассматриваемого частного случая.
Если 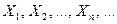– попарно независимые случайные величины, имеющие одно и то же математическое ожидание 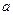, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число 
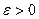, вероятность неравенства
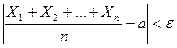
будет как угодно близка к единице, если число случайных величин достаточно велико.
Сущность теоремы Чебышева заключается в том, что хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу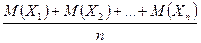 
(или к числу 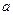в частном случае). Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.
Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть, какое значение примет их среднее арифметическое.
Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются.
Теорема Чебышева справедлива не только для дискретных, но и для непрерывных случайных величин.
На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемое сотнями.
В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зерен мало сравнительно со всей массой зерна, но само по себе оно достаточно велико.
