равило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией.
Множество Х называется областью определения функции.
Множество Y называется множеством значений значений функции.
Равенство  называется уравнением функции. В этом уравнении
называется уравнением функции. В этом уравнении  - независимая переменная, или аргумент функции.
- независимая переменная, или аргумент функции. 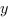 - зависимая переменная.
- зависимая переменная.
Если мы возьмем все пары  и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции – это графической изображение зависимости между множествами Х и Y.
и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции – это графической изображение зависимости между множествами Х и Y.
Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.
Основные свойства функций.
1. Область определения функции.
Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции  имеет смысл. Другими словами, это область допустимых значений выражения
имеет смысл. Другими словами, это область допустимых значений выражения  .
.
Чтобы по графику функции  найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.
2. Множество значений функции.
Множество значений функции Е(y)- это множество всех значений, которые может принимать зависимая переменная y.
Чтобы по графику функции  найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.
3. Нули функции.
Нули функции – это те значения аргумента х, при которых значение функции (y) равно нулю.
Чтобы найти нули функции  , нужно решить уравнение
, нужно решить уравнение  . Корни этого уравнения и будут нулями функции
. Корни этого уравнения и будут нулями функции  .
.
Чтобы найти нули функции  по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции
по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции  .
.
4. Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции  – это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть 0
– это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть 0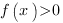 и
и  .
.
Чтобы найти промежутки знакопостоянства функции  по ее графику, нужно
по ее графику, нужно
- найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ – при этих значениях аргумента
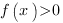
- найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ – при этих значениях аргумента

5. Промежутки монотонности функции.
Промежутки монотонности функции  – это такие промежутки значений аргумента х, при которых функция
– это такие промежутки значений аргумента х, при которых функция  возрастает или убывает.
возрастает или убывает.
Говорят, что функция  возрастает на промежутке I, если для любых двух значений аргумента
возрастает на промежутке I, если для любых двух значений аргумента  , принадлежащих промежутку I таких, что
, принадлежащих промежутку I таких, что  выполняется соотношение:
выполняется соотношение:  .
.
Другими словами, функция  возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Чтобы по графику функции  определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которыхграфик идет вверх.
определить промежутки возрастания функции, нужно, двигаясь слева направо по линии графика функции, выделить промежутки значений аргумента х, на которыхграфик идет вверх.
Говорят, что функция  убывает на промежутке I, если для любых двух значений аргумента
убывает на промежутке I, если для любых двух значений аргумента  , принадлежащих промежутку I таких, что
, принадлежащих промежутку I таких, что  выполняется соотношение:
выполняется соотношение:  {f(x)}» title=»{f(x_0)}>{f(x)}»/>.
{f(x)}» title=»{f(x_0)}>{f(x)}»/>.
Графически это означает что точка с абсциссой 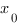 лежит выше других точек из окрестности I графика функции
лежит выше других точек из окрестности I графика функции  .
.
Точка 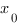 называется точкой минимума функции
называется точкой минимума функции  , если существует такая окрестность I точки
, если существует такая окрестность I точки 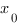 , что для любой точки х из этой окрестности выполняется соотношение:
, что для любой точки х из этой окрестности выполняется соотношение:


Графически это означает что точка с абсциссой 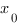 лежит ниже других точек из окрестности I графика функции
лежит ниже других точек из окрестности I графика функции  .
.
Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.
7. Четность (нечетность) функции.
Функция  называется четной, если выполняются два условия:
называется четной, если выполняются два условия:
а) Для любого значения аргумента  , принадлежащего области определения функции,
, принадлежащего области определения функции,  также принадлежит области определения функции.
также принадлежит области определения функции.
Другими словами, область определения четной функции  симметрична относительно начала координат.
симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение  .
.
Функция  называется нечетной, если выполняются два условия:
называется нечетной, если выполняются два условия:
а) Для любого значения аргумента  , принадлежащего области определения функции,
, принадлежащего области определения функции,  также принадлежит области определения функции.
также принадлежит области определения функции.
Другими словами, область определения нечетной функции  симметрична относительно начала координат.
симметрична относительно начала координат.
б) Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение  .
.
Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.
Чтобы определить четность функции, нужно:
а). Найти область определения функции  , и определить, является ли она симметричным множеством.
, и определить, является ли она симметричным множеством.
Если, например, число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция  – функция общего вида.
– функция общего вида.
Если область определения функции  – симметричное множество, то проверяем п. б)
– симметричное множество, то проверяем п. б)
б). В уравнение функции  нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду
нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду  или
или  .
.
Если  , то функция четная.
, то функция четная.
Если  , то функция нечетная.
, то функция нечетная.
Если не удалось привести ни к тому ни к другому, то наша функция  – общего вида.
– общего вида.
График четной функции симметричен относительно оси ординат ( прямой OY ).
График нечетной функции симметричен относительно начала координат ( точки (0,0) ).
8. Периодичность функции.
Функция  называется периодической, если существует такое положительное число Т, что
называется периодической, если существует такое положительное число Т, что
- для любого значения х из области определения функции, х+Т также принадлежит D(x)

В программе средней школы из числа периодических функций изучают только тригонометрические функции.

