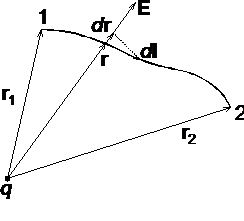Существуют два равнозначных определения консервативной силы. Оба они подробно обсуждались в механике.
-
Консервативной называется сила, работа которой не зависит от формы траектории.
-
Консервативной называется сила, работа которой на замкнутой траектории равна нулю.
Рассмотрим перемещение заряда q в электростатическом поле по замкнутой траектории (рис. 3.5.). Заряд из точки 1 перемещается по пути L1 в точку 2, а затем возвращается в исходное положение по другому пути L2. В процессе этого движения на заряд со стороны поля действует консервативная электрическая сила:
.
Работа этой силы на замкнутой траектории L = L1 + L2 равна нулю:
.
Это уравнение, упростив, запишем так:
. (3.18)
Рис. 3.5.
Разберём подробно последнее уравнение. Подынтегральное выражение — элементарная работа электрической силы, действующей на единичный положительный заряд, на перемещении (рис. 3.6.):
, (3.19)
здесь q = 1 — единичный заряд.
Рис. 3.6.
При подсчёте работы на замкнутой траектории необходимо сложить элементарные работы электрической силы на всех участках траектории. Иными словами, проинтегрировать (3.19) по замкнутому контуру L:
. (3.20)
Интеграл по замкнутому контуру =
называется циркуляцией вектора напряжённости электростатического поля по контуру L. По своей сути циркуляция вектора напряжённости — это работа электростатического поля, совершаемая при перемещении по замкнутому контуру единичного положительного заряда.
Так как речь идёт о работе консервативной силы, то на замкнутой траектории она равна нулю:
.
Теорема о циркуляции в электростатике: циркуляция вектора напряжённости электростатического поля по любому замкнутому контуру равна нулю.
Работа перемещения заряда. На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила
F = q E. При перемещении заряда на отрезке dl силами поля совершается работа
dA = F dl = q E dl cos (E, dl).
При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна
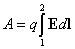 .
.
Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого
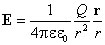 .
.
Проекция отрезка dl на направление вектора E (рис. 1.5) есть dr = dl cos (E, dl).
Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:
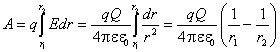
|
|
Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении.
Для электрического поля, созданного системой зарядов Q1, Q2,¼, Qn, работа перемещения заряда q равна алгебраической сумме работ составляющих сил:
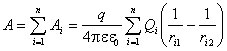 .
.
Таким же образом, как и каждая из составляющих работ, суммарная работа зависит только от начального и конечного положений заряда q.
Циркуляция вектора напряженности электрического поля. Работа, совершаемая силами электрического поля при перемещении единичногоположительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:
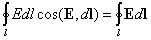
Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.
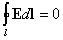 .
.
Равенство нулю означает, что силы электрического поля являются силамиконсервативными, а само поле - потенциальным.