Сложная функция – это функция, аргументом которой также является функция.
Формула нахождения производной сложной функции.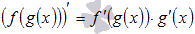
"Двухслойная" сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.
Если f и g - дифференцируемые функции, то сложная функция 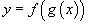 также дифференцируема по x и ее производная равна
также дифференцируема по x и ее производная равна
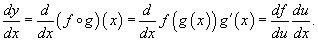
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!
Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.
Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.
Предполагается, что основание a показательной и логарифмической функции больше нуля и не равно единице: a > 0, a ≠ 1. Производная показательной функции y = ax с основанием a определяется формулой
 где ln a - натуральный логарифм a, т.е. логарифм a по основанию е, приблизительно равному 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Знаменитое трансцендентное число е можно вычислить с любой степенью точности с помощью различных компьютерных алгоритмов.
где ln a - натуральный логарифм a, т.е. логарифм a по основанию е, приблизительно равному 2,718281828... (2.7, затем два раза год рождения Л.Н.Толстого). Знаменитое трансцендентное число е можно вычислить с любой степенью точности с помощью различных компьютерных алгоритмов.
Если a = е, то получаем красивый результат в виде

Если a = е, то получаем красивый результат в виде

Производная логарифмической функции y = loga x определяется выражением
 Для натурального логарифма y = ln x производная равна
Для натурального логарифма y = ln x производная равна




