Понятие производной, ее геометрический и механический смысл
Определение:
Средней скоростью изменения функции  при переходе независимой переменной от значения
при переходе независимой переменной от значения  к значению
к значению 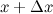 называется отношение приращения
называется отношение приращения 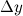 функции к приращению
функции к приращению 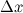 независимой переменной, то есть
независимой переменной, то есть
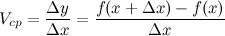
Определение:
Истинной или мгновенной скоростью изменения функции  при заданном значении независимой переменной
при заданном значении независимой переменной  называется предел, к которому стремится средняя скорость изменения функции при стремлению к нулю приращения аргумента
называется предел, к которому стремится средняя скорость изменения функции при стремлению к нулю приращения аргумента 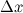 :
:
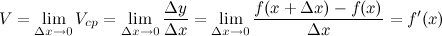
1.Механический смысл производной
Теорема:
Пусть задан путь 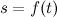 движения материальной точки. Скорость данной материальной точки в момент времени
движения материальной точки. Скорость данной материальной точки в момент времени 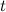 есть производная от пути
есть производная от пути  по времени
по времени 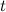 :
:
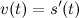
Пример:
Задание. Тело движется прямолинейно по закону 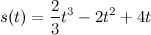 (м). Определить скорость его движения в момент
(м). Определить скорость его движения в момент 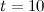 с.
с.
Решение. Искомая скорость - это производная от пути, то есть
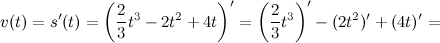
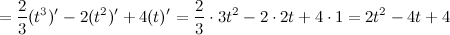
В заданный момент времени
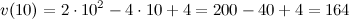 (м/с).
(м/с).
Ответ. 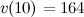 (м/с).
(м/с).
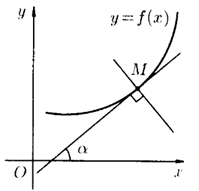
2.Геометрический смысл производной
Производная функции  , вычисленная при заданном значении
, вычисленная при заданном значении  , равна тангенсу угла, образованного положительным направлением оси
, равна тангенсу угла, образованного положительным направлением оси 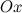 и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой
и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой  :
:
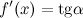
Замечание:
Геометрически производная представляет собой угловой коэффициент касательной к графику функции в точке
в точке 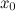 .
.
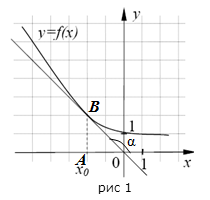
Пример:
Задание. На рисунке №1 изображен график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 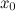 . Найти значение
. Найти значение 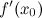 .
.
Решение. Из геометрического смысла производной получаем, что
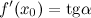
Найдем угол 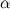 . Рассмотрим треугольник
. Рассмотрим треугольник 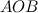 - прямоугольный, равнобедренный. Тогда
- прямоугольный, равнобедренный. Тогда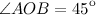 , а значит
, а значит
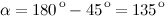
А отсюда следует, что
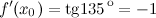
Ответ. 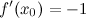
Уравнение касательной к графику функции
Ключевые слова: касательная, прямая, производная, функция, угловой коэффициент
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке  f=f(x0+
f=f(x0+ x)−f(x0) к приращению аргумента
x)−f(x0) к приращению аргумента  x
x
при  x
x 0: f
0: f (x0)=lim
(x0)=lim x
x 0
0 xf(x0+
xf(x0+ x)−f(x0).
x)−f(x0).
Геометрический смысл производной
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Вычисление производной функции
Таблица производных элементарных функций
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Вычислите производные следующих функций:
а)  ;
;
б) ![f(x)=\sqrt[3]{x} f(x)=\sqrt[3]{x}](http://hijos.ru/wp-content/ql-cache/quicklatex-415c4f39a1a68ccac15da99969baacfc.gif) ;
;
в) ![f(x)=x^2\sqrt[4]{x^5} f(x)=x^2\sqrt[4]{x^5}](http://hijos.ru/wp-content/ql-cache/quicklatex-f8486d1f7d35a350b153948070bec396.gif) ;
;
г)  ;
;
д)  .
.
Примеры не дифференцируемых функций в точке
Исходя из определения, докажем, что функция y = x2 дифференцируема в точке x0 = 3.
Решение.
Функция называется дифференцируемой в точке x0, если ее приращение представимо в виде
| Δf = f(x0 + Δx) − f(x0) = A · Δx + o(Δx) , |
где A — число, не зависящее от Δх, а o(Δx) — функция более высокого порядка малости, чем Δx, при Δx → 0 .
В нашем случае приращение функции y = x2 в точке x0 =3 имеет вид
| Δf = (3 + Δx)2 − 9 = 6 · Δx + (Δx)2 . |
Таким образом, приращение Δf есть сумма линейной относительно Δx части, равной 6 · Δx, и бесконечно малой (Δx)2 второго (более высокого, чем Δx) порядка малости при Δx → 0. Следовательно, по определению функция y = x2 дифференцируема в точке x = 3.

