Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
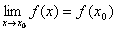
Тот же факт можно записать иначе: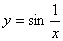 
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию
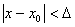
верно неравенство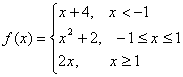 
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x)
где a(х) – бесконечно малая при х®х0.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций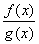 
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Свойства функций, непрерывных на отрезке.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M £ f(x) £ M.
Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.
Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем
m £ f(x) £ M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.
Т.е. если sign(f(a)) ¹ sign(f(b)), то $ х0: f(x0) = 0.
Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого e>0 существует D>0 такое, что для любых точек х1Î[a,b] и x2Î[a,b] таких, что
ïх2 – х1ï< D
верно неравенство ïf(x2) – f(x1)ï < e
Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое D, не зависящее от х, а при “обычной” непрерывности D зависит от e и х.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.
Приращение аргумента и функции
На оси Х – две точки: x0 и x1 (рис.1). Если от x1 отнимем x0, то узнаем длину шага между ними – а говоря иначе, узнаем, на сколько приросла точка x0 в точке x1. Эта разность между двумя заданными точками оси X и называется приращением аргумента.
Точки x0 и x1 образуют на оси Y соответственно точки у0 и у1. Если от у1 отнять у0, то мы получим приращение функции.
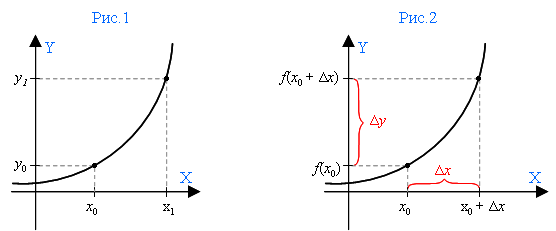
Итак, в функции y = f(x) относительно определенных точек x0 и x1:
разность x1 – x0 называется приращением аргумента, а разность у1 – у0 называется приращением функции.
Но у0 и у1 – зависимые переменные (зависимые от значений х). То есть их правильно записывать так:f(x0) и f(x1). Следовательно, приращение функции – это разность f(x1) – f(x0).
Приращение обозначается греческой буквой Δ (дельта):
Δx = x1 – x0;
Δy (или Δ f) = f(x1) – f(x0).
Можно сказать и иначе: если к x0 прибавить величину приращения Δx, то мы получим точку x1.
То есть x1 = x0 + Δx (рис.2).
Тогда точку f(x1), отмеченную на первом рисунке как у1, тоже можно обозначить иначе:
f(x0 + Δx).
Осталось вывести формулу приращения функции.
Формула приращения функции:
Δy = f(x0 + Δx) – f(x0)
или
Δf = f(x0 + Δx) – f(x0)
Пример: Дана функция y = x2. На оси абсцисс – две точки:
х0 = 3,
(х0 + Δx) = 4.
Надо найти приращение функции при переходе от точки х0 к точке (х0 + Δx).
Решение.
Итак, мы хотим найти Δy.
Сначала определимся с функцией:
так как у = f(x), то f(x) = x2.
Теперь вычисляем приращение аргумента:
Δx = (х0 + Δx) – х0 = 4 – 3 = 1
Находим значения функции при х0 = 3 и (х0 + Δx) = 4:
f(x0) = f(3) = 32 = 9
f(x0 + Δx) = f(4) = 42 = 16
Осталось найти приращение функции:
Δy = f(x0 + Δx) – f(x0) = f(4) – f(3) = 16 – 9 = 7.
Ответ: Δy = 7.
