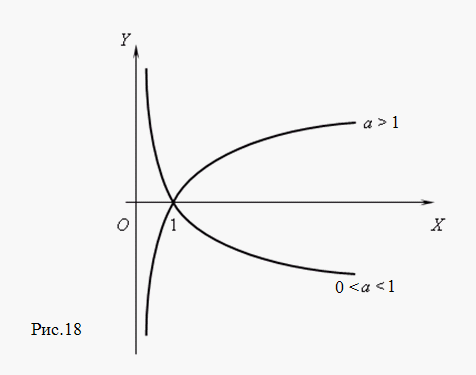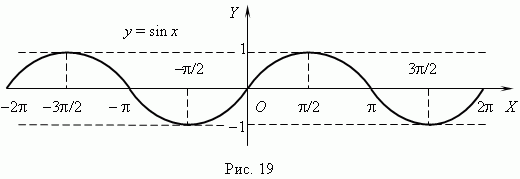1.Пропорциональные величины.
Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k x ,где k - постоянная величина ( коэффициент пропорциональности ).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол 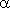 , тангенс которого равен k : tan
, тангенс которого равен k : tan 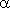 = k. Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3 .
= k. Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3 .
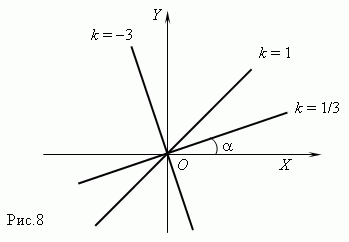
2.Линейная функция.
Если переменные y и x связаны уравнением 1-ой степени:
A x + B y = C ,
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
3.Обратная пропорциональность.
Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением:
y = k / x ,
где k - постоянная величина.
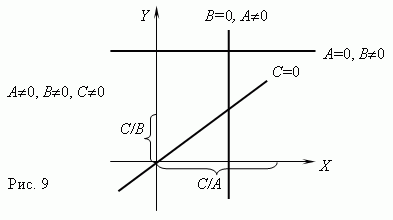
График обратной пропорциональности – гипербола ( рис.10 ). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конусаплоскостью ( о конических сечениях см. раздел «Конус» в главе «Стереометрия» ). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy =k.
Основные характеристики и свойства гиперболы:
- область определения функции: x  0, область значений: y
0, область значений: y  0 ;
0 ;
- функция монотонная ( убывающая ) при x < 0 и при x > 0, но не
монотонная в целом из-за точки разрыва x = 0 ( подумайте, почему ? );
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
4.Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a  0. В простейшем случае: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
0. В простейшем случае: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
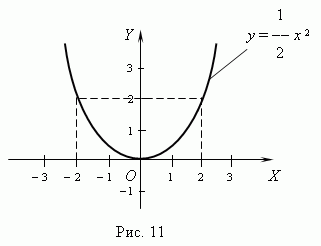
График функции y = ax 2 + bx + c - тоже квадратная парабола того же вида, что и y = ax 2, но её вершина лежит не в начале координат, а в точке с координатами:
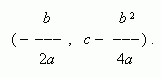
Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x2 идискриминанта D = b2 – 4ac. Эти свойства следуют из анализа корней квадратного уравнения.
Все возможные различные случаи для квадратной параболы показаны на рис.12.
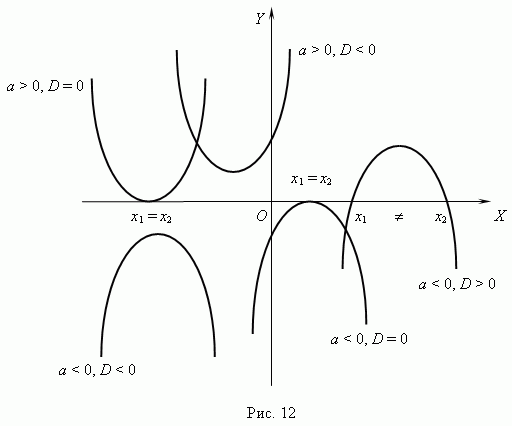
Изобразите, пожалуйста, квадратную параболу для случая a > 0, D > 0 .
Основные характеристики и свойства квадратной параболы:
- область определения функции: - 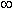 < x < +
< x < + 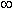 ( т.e. x
( т.e. x 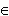 R ), а область
R ), а область
значений: … (ответьте, пожалуйста, на этот вопрос сами !);
- функция в целом не монотонна, но справа или слева от вершины
ведёт себя, как монотонная;
- функция неограниченная, всюду непрерывная, чётная при b = c = 0,
и непериодическая;
- при D < 0 не имеет нулей. ( А что при D 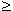 0 ? ) .
0 ? ) .
| 5. |
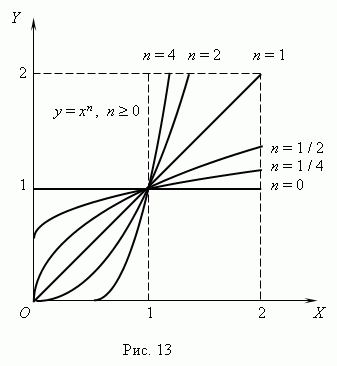
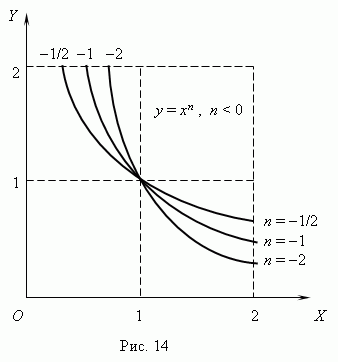
Степенная функция. Это функция: y = axn, где a, n – постоянные. При n = 1 получаем прямую пропорциональность: y = ax; при n = 2 -квадратную параболу ; при n = -1 - обратную пропорциональность или гиперболу. Таким образом, эти функции - частные случаи степеннойфункции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, cледовательно, приn = 0 степенная функция превращается в постоянную величину: y = a, т.e. её график - прямая линия, параллельная оси Х, исключая начало координат ( поясните, пожалуйста, почему ? ).Все эти случаи ( при a = 1 ) показаны на рис.13 ( n
Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.
При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой. На рис.16 представлена функция |
| 6. |
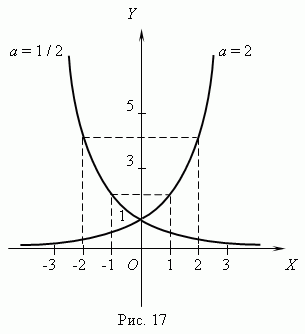
Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией. Аргумент x принимаетлюбые действительные значения; в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию. Так, функция y = 81x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i (проверьте,пожалуйста !). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку ( 0, 1 ). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает.
Основные характеристики и свойства показательной функции: - область определения функции: - область значений: y > 0 ; - функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - нулей функция не имеет.
|
| 7. |
Логарифмическая функция. Функция y = log a x, где a – постоянное положительное число, не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график ( рис.18 ) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Основные характеристики и свойства логарифмической функции: - область определения функции: x > 0, а область значений: - ( т.e. y - это монотонная функция: она возрастает при a > 1 и убывает при 0 < a < 1; - функция неограниченная, всюду непрерывная, непериодическая; - у функции есть один ноль: x = 1. |
| 8. |
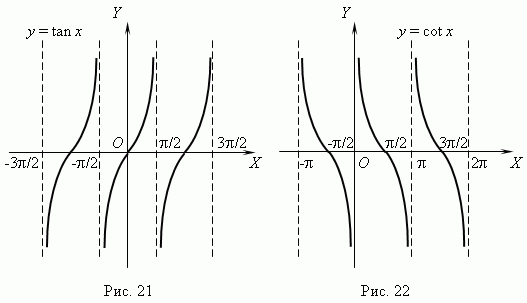
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов. Тогда функция y= sin x представляется графиком ( рис.19 ). Эта кривая называется синусоидой.
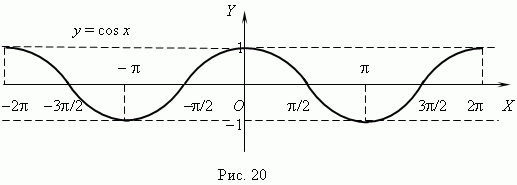
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на
|
| 9. |
Обратные тригонометрические функции. Определения обратных тригонометрических функций и их основные свойства приведены водноимённом разделе в главе «Тригонометрия». Поэтому здесь мы ограничимся лишь короткими комметариями, касающимися их графиков, полученных поворотом графиков тригонометрических функций вокруг биссектрисы 1-го координатного угла.
|
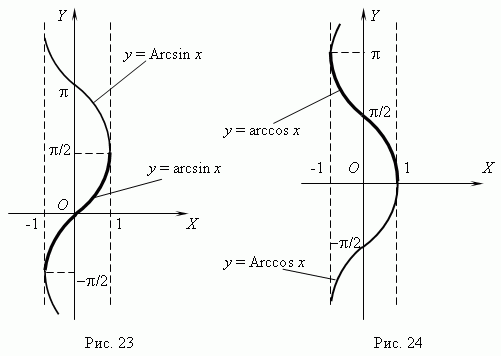
Функции y = Arcsin x ( рис.23 ) и y = Arccos x ( рис.24 ) многозначные, неограниченные; их область определения и область значений соответственно: -1  x
x  +1 и -
+1 и - 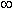 < y < +
< y < + 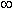 . Поскольку эти функции многозначные,не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
. Поскольку эти функции многозначные,не рассматриваемые в элементарной математике, в качестве обратных тригонометрических функций рассматриваются их главные значения: y = arcsin x и y = arccos x; их графики выделены на рис.23 и рис.24 жирными линиями.
Функции y = arcsin x и y = arccos x обладают следующими характеристиками и свойствами:
- у обеих функций одна и та же область определения: -1  x
x  +1 ;
+1 ;
их области значений: - /2
/2  y
y 
 /2 для y = arcsin x и 0
/2 для y = arcsin x и 0  y
y 
 для y = arccos x;
для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arcsin x – возрастающая функция; y = arccos x – убывающая );
- каждая функция имеет по одному нулю ( x = 0 у функции y = arcsin x и
x = 1 у функции y = arccos x).
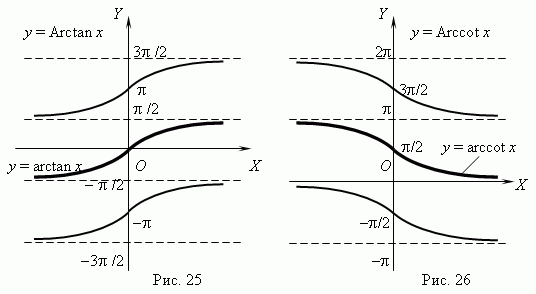
Функции y = Arctan x ( рис.25 ) и y = Arccot x ( рис.26 ) - многозначные, неограниченные; их область определения: - 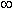
 x
x  +
+ 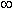 . Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
. Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.
Функции y = arctan x и y = arccot x имеют следующие характеристики и свойства:
- у обеих функций одна и та же область определения: - 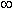
 x
x  +
+ 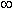 ;
;
их области значений: - /2 < y <
/2 < y <  /2 для y = arctan x и 0 < y <
/2 для y = arctan x и 0 < y <  для y = arccos x;
для y = arccos x;
- функции ограниченные, непериодические, непрерывные и монотонные
( y = arctan x – возрастающая функция; y = arccot x – убывающая );
- только функция y = arctan x имеет единственный ноль ( x = 0 );
функция y = arccot x нулей не имеет.


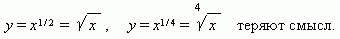
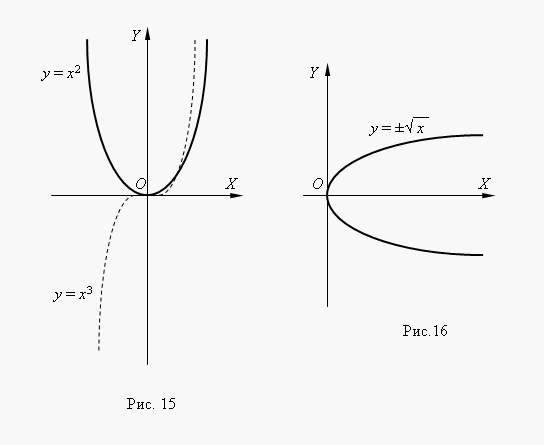
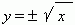 . Эта функция является обратной к квадратной параболе y = x 2, её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла. Это способ получения графика любой обратной функции из графика её исходной функции. Мы видим по графику, что это двузначная функция (об этом говорит и знак ± перед квадратным корнем). Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.
. Эта функция является обратной к квадратной параболе y = x 2, её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла. Это способ получения графика любой обратной функции из графика её исходной функции. Мы видим по графику, что это двузначная функция (об этом говорит и знак ± перед квадратным корнем). Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.