Определение функции: Если каждому числу х из множества чисел D поставлено в соответствие единственное число у, то говорят, что на множестве D задана функция f и пишут y= f(x), где х - называется независимой переменной или аргументом этой функции, а множество D - область определения этой функции.
Все значения, которые принимает функция f(x) (при х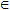 D), образуют область значения (изменения) функции Е.
D), образуют область значения (изменения) функции Е.
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Существует три способа задания функции: табличный, аналитический, графический.
Табличный способ задания функции состоит в том, что для каждого значения аргумента х рядом выписывается соответствующее значение у, получается таблица. Например:
С точки зрения математики здесь изучается зависимость между определенными переменными, другими словами изучается некоторая функция. При опыте ведутся записи, в простейшем случае отмечается время (аргумент функции) и записывается показание прибора (соответствующее значение функции), т.е. функция задается таблицей. А задача исследователя состоит в том, чтобы по полученной таблице изучить функцию.
Способ задания функции с помощью формулы у=f(х), где f(x) некоторое выражение с переменной х - называется аналитическим способом.
Пример 1. Функция у=f(х) задана аналитической формулой:
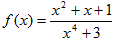
Найти f(-х), f(|х|).
Чтобы найти f(-х), надо в f(х) всюду вместо х подставить (-х). Получим:
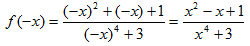 . Аналогично находим и для f(|х|).
. Аналогично находим и для f(|х|).
Пример 2. Найти область определения функции 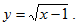
Выражение вида 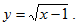 определено при тех х, для которых х-1
определено при тех х, для которых х-1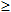 0, т.е. при х
0, т.е. при х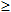 1
1
Значит, область определения функции - луч [1,+∞).
Пример 3. Найти области определения и значений функции y=lg(4-3x-x2).
Логарифмическая функция определена, если 4-3x-x2>0. Корни квадратного трехчлена: x1=-4, x2=1. Записанное выше неравенство равносильно неравенству -(x+4)(x-1)>0 , что возможно при x>4 и x<1. Область определения данной функции есть интервал (-4;1). Так как в D 0<4-3x-x2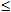 25/4, то интервал (-∞ ;lg(25/4)) - область значения функции.
25/4, то интервал (-∞ ;lg(25/4)) - область значения функции.
Способы задания функций
Функция может быть задана тремя способами: аналитическим, табличным и в виде графика.
2.1 Аналитический способ задания функции
Функция задается в виде аналитического выражения или формулы, содержащей указания на операции или действия над константами и аргументом x, чтобы получить соответствующие значения y.
Аналитический способ задания функций является наиболее важным в математике, физике и прикладных науках, в которых математика служит инструментом. В “нематематических” науках, например, в химии формулы или аналитические выражения носят информационный характер.
Например:
в математике: y = kx + b; y = sin x и т.д.
в физике: F = ma; E = mc2 и т.д.
в химии: H2O; C2H5OH и т.д.
2.2 Табличный способ задания функций
Аргумент и вычисляемая функция записываются в таблицу. Форма таблицы может быть вертикальной или горизонтальной.
| x | |||||||
| y |
Подобным образом создаются различные справочные таблицы для быстрого нахождения каких либо величин, выраженных аналитически, например, таблицы логарифмов, степеней, тригонометрических функций и т. д. или, как запись экспериментальных исследований, по которым может быть найдена эмпирическая формула или построен график.
Таблицы широко применяются в технике, производстве, военном деле, навигации и т. д. Их использование значительно сокращает время принятия решения человеком в его профессиональной деятельности.
2.3 Графический способ задания функций
Графический способ задания функции является наиболее наглядным и часто применяется в технике. Самописцы и многоканальные шлейфовые осцилографы дают изображение графика (графиков) на бумагу, например, с датчиков, установленных на теле человека при снятии электрокардиограммы сердца. Электронные осцилографы выдают изображение графика на экран электронно-лучевой трубки.
В математическом анализе графический способ задания функций используется в качестве иллюстрации.
Пример. Пусть S - площадь квадрата, a - сторона квадрата. Необходимо изучить, как изменяется площадь квадрата при изменении размеров его сторон?
Задавая значения сторон квадрата, вычисляем его площадь. Следовательно, размер стороны квадрата будет являться аргументом, а вычисленное значение площади квадрата функцией, т.е. имеем формулу:
S = a2
Результаты расчетов записываем в таблицу:
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| S | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
По данным таблицы строим график:
.gif)
В этом примере проиллюстрированы три способа задания функции: аналитический, табличный и графический.
Четность, нечетность функции
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.
Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Четные функции обладают сойством: ƒ(–x)=ƒ(x).
А нечетные: g(–x)=–g(x).(меняется знак)
- Функция
![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](http://static4.wikia.nocookie.net/__cb62501/math/ru/images/math/e/d/5/ed5743482e96ed8c5bee8117ee026844.png) называется нечётной, если справедливо равенство
называется нечётной, если справедливо равенство
![f(-x)=-f(x), \quad \forall x \in [-X,X].](http://static1.wikia.nocookie.net/__cb62501/math/ru/images/math/f/6/a/f6ab611fbaf32ad9e732deb96e3fb9ca.png)
- Функция
 называется чётной, если выполнено равенство
называется чётной, если выполнено равенство
![f(-x) = f(x),\quad \forall x \in [-X,X].](http://static1.wikia.nocookie.net/__cb62501/math/ru/images/math/7/1/2/712740b91f011d49b277240b725bef17.png)
- Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Свойства:
- График нечётной функции симметричен относительно начала координат
 .
. - График чётной функции симметричен относительно оси ординат
 .
. - Произвольная функция
![f:[-X,X] \subset \mathbb{R} \to \mathbb{R}](http://static4.wikia.nocookie.net/__cb62501/math/ru/images/math/e/d/5/ed5743482e96ed8c5bee8117ee026844.png) может быть представлена в виде суммы нечётной и чётной функций:
может быть представлена в виде суммы нечётной и чётной функций:

где

- Функция
 — единственная функция, одновременно являющаяся нечётной и чётной.
— единственная функция, одновременно являющаяся нечётной и чётной. - Сумма двух нечётных функций сама нечётна.
- Сумма двух чётных функций сама чётна.
- Произведение или дробь двух нечётных функций чётно.
- Произведение или дробь двух чётных функций чётно.
- Произведение или дробь нечётной и чётной функций нечётно.
- Композиция двух нечётных функция нечётна.
- Композиция двух чётных функций чётна.
- Композиция чётной функции с нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот).
Примеры:
Нечётные функции:
- функции с нечетными степенями
- .y=sin x, y=tg x, y=ctg x
Чётные функции:
- Чётная степень
 где
где  — произвольное целое число.
— произвольное целое число. - Косинус
 .
.
Монотонность функции
Определение 1: Функции  называется возрастающей [убывающей] на множестве
называется возрастающей [убывающей] на множестве  , если для любых значений аргумента
, если для любых значений аргумента  из
из 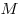 выполняется условие
выполняется условие 
![[x_2 > x_1 \Rightarrow f(x_2 ) < f(x_1 )] [x_2 > x_1 \Rightarrow f(x_2 ) < f(x_1 )]](http://www.fmclass.ru/inc/pictures/b5f13aa6c66060934e796b7e8914f840.png) .
.
Определение 2: Промежутки области определения, на которых функция возрастает или убывает, называются промежутками монотонности функции.
Определение 3: Функция  называется возрастающей [убывающей], если для любых значений аргумента
называется возрастающей [убывающей], если для любых значений аргумента  из
из  выполняется условие
выполняется условие 
![[x_2 > x_1 \Rightarrow f(x_2 ) < f(x_1 )] [x_2 > x_1 \Rightarrow f(x_2 ) < f(x_1 )]](http://www.fmclass.ru/inc/pictures/5e6804784b5a0d6b5a05e845f2fea87f.png) .
.
Определение 4: Возрастающие и убывающие функции называются монотонными.
-
Свойство 1. Пусть функция
 возрастает (убывает) на множестве
возрастает (убывает) на множестве 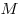 и С – любое число. Тогда функция
и С – любое число. Тогда функция  , также возрастает (убывает) на множестве
, также возрастает (убывает) на множестве 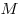 .
. -
Свойство 2. Пусть функция
 возрастает (убывает) на множестве
возрастает (убывает) на множестве 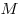 и C > 0. Тогда функция
и C > 0. Тогда функция  , также возрастает (убывает) на множестве
, также возрастает (убывает) на множестве 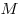 .
. -
Свойство 3. Пусть функция
 возрастает (убывает) на множестве
возрастает (убывает) на множестве 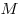 и C < 0. Тогда функция
и C < 0. Тогда функция  , убывает (возрастает) на множестве
, убывает (возрастает) на множестве 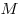 .
. -
Свойство 4. Пусть функция
 возрастает (убывает) и знакопостоянна на множестве
возрастает (убывает) и знакопостоянна на множестве 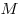 . Тогда функция
. Тогда функция  , убывает (возрастает) на множестве
, убывает (возрастает) на множестве 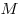 .
. -
Свойство 5. Сумма возрастающих (убывающих) функций есть функция возрастающая (убывающая).
-
Свойство 6. Произведение возрастающих (убывающих) неотрицательных функций есть функция возрастающая (убывающая).
Теорема 1. Если функция  возрастает на множестве
возрастает на множестве 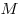 , а функция
, а функция 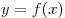 убывает на множестве
убывает на множестве 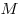 , то уравнение
, то уравнение  имеет на
имеет на 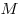 не более одного корня.
не более одного корня.
Теорема 2. Если функция  монотонна на множестве
монотонна на множестве 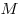 , а функция
, а функция 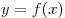 постоянна на множестве
постоянна на множестве 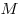 , то уравнение
, то уравнение  имеет на
имеет на  не более одного корня.
не более одного корня.
Периодичность функции
Функция  называется периодической, если существует такое число
называется периодической, если существует такое число  , что выполнены два условия:
, что выполнены два условия:
- Вместе с любым
 область определения функции содержит числа
область определения функции содержит числа  и
и  .
. - Для любого
 верны равенства
верны равенства  .
.
Число  называется периодом функции. Как правило, говоря "период" функции подразумевают наименьший положительный период.
называется периодом функции. Как правило, говоря "период" функции подразумевают наименьший положительный период.
Замечание. Если известно, что функция периодическая и известен её период  , то исследование функции достаточно провести на любом отрезке длины
, то исследование функции достаточно провести на любом отрезке длины  .
.
Примеры.
 . Период:
. Период:  ,
,  ,
,  ,
,  . Период:
. Период:  ,
,  ,
,  .
.
Дробная часть  :
:  . Период — любое целое число, кроме нуля.
. Период — любое целое число, кроме нуля.
Константа, например,  . Период — любое число, кроме нуля.
. Период — любое число, кроме нуля.
Наименьший положительный период функции
Пусть дана периодическая функция  . Если
. Если  — период функции, то из определения следует, что
— период функции, то из определения следует, что  ;
;  и т.п., то есть числа вида
и т.п., то есть числа вида  ,
,  ,
,  также являются периодами. При исследовании функции важно среди всех периодов найти наименьший положительный период, если он существует. Наименьший положительный период ещё называется главным или основным периодом.
также являются периодами. При исследовании функции важно среди всех периодов найти наименьший положительный период, если он существует. Наименьший положительный период ещё называется главным или основным периодом.
Примеры.
- Синус:
 . Главный период:
. Главный период:  ,
, - Дробная часть
 :
:  .
.  .
.  . Главный период не существует.
. Главный период не существует.- Функция Дирихле. Период — любое рациональное число, кроме нуля. Главный период не существует.
График периодической функции

График периодической функции состоит из одинаковых фрагментов, каждый из которых имеет длину, равную периоду функции. График функции, имеющей главный период  удобно построить на любом отрезке длины
удобно построить на любом отрезке длины  , а затем полученный график сдвигать вдоль оси
, а затем полученный график сдвигать вдоль оси  вправо и влево на расстояния
вправо и влево на расстояния  ,
,  ,
,  и т.д.
и т.д.

