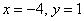Метод Гаусса
Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу!
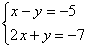 и решим ее методом Гаусса.
и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы: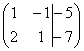
Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: 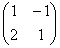 . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:
. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: 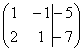 . Любую из матриц можно для краткости называть просто матрицей.
. Любую из матриц можно для краткости называть просто матрицей.
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: 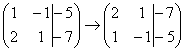
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу  . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:
. В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: 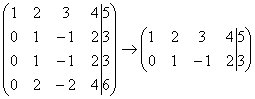 .
.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу 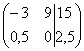 . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:
. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: 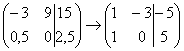 . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: 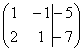 . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2:
. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: 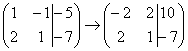 , и ко второй строке прибавляем первую строку умноженную на –2:
, и ко второй строке прибавляем первую строку умноженную на –2: 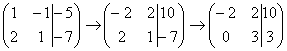 . Теперь первую строку можно разделить «обратно» на –2:
. Теперь первую строку можно разделить «обратно» на –2: 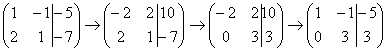 . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
. Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: 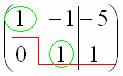
В результате элементарных преобразований получена эквивалентная исходной система уравнений: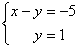
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.
В нижнем уравнении у нас уже готовый результат: 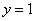 .
.
Рассмотрим первое уравнение системы 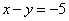 и подставим в него уже известное значение «игрек»:
и подставим в него уже известное значение «игрек»: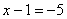
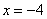
Ответ: