Экстремумом функции называется максимальное (минимальное) значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума.
Теорема (необходимое условие экстремума)
Если точка — точка экстремума функции
, то она критическая.
Доказательство: По условию точка  — точка экстремума функции
— точка экстремума функции 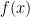
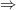 по теореме Фермапроизводная
по теореме Фермапроизводная 
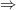 точка
точка  является критической.
является критической.
Замечания: Не всякая критическая точка является точкой экстремума.
Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция дифференцируема в некоторой окрестности точки
, кроме, быть может, самой точки
и непрерывна в этой точке. Тогда:
- Если производная
меняет знак с «-» на «+» при переходе через точку
:
и
, то
— точка строго минимума функции
- Если производная
меняет знак с «+» на «-» при переходе через точку
:
и
, то
— точка строго максимума функции
Доказательство: Пусть, например,  меняет знак с «-» на «+». Рассмотрим точку
меняет знак с «-» на «+». Рассмотрим точку  на сегменте
на сегменте ![\left [ x;x_{0} \right ]. \left [ x;x_{0} \right ].](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+x%3Bx_%7B0%7D+%5Cright+%5D.&bg=ffffff&fg=000&s=0) Воспользуемся теоремой о конечных приращениях Лагранжа:
Воспользуемся теоремой о конечных приращениях Лагранжа: 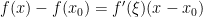 ,
,  . Поскольку при переходе через точку
. Поскольку при переходе через точку  функция меняет знак с «-» на «+», то
функция меняет знак с «-» на «+», то  и
и  , то
, то 

Аналогично рассмотрим сегмент , получим
— точка строгого минимума функции.
Замечания: Если  — точка строго экстремума, то из этого не следует, что производная
— точка строго экстремума, то из этого не следует, что производная 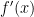 меняет знак при переходе через точку
меняет знак при переходе через точку 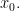
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть дана функция , ее первая производная
и пусть
, тогда:
- Если
, то точка
— точка строгого минимума;
- Если
, то точка
— точка строгого максимума.
Доказательство: Докажем теорему для первого случая, когда 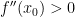 . По скольку
. По скольку  непрерывна, то на достаточно малом интервале
непрерывна, то на достаточно малом интервале  , т.к
, т.к 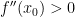 , то
, то  возрастает в этом интервале.
возрастает в этом интервале.  , значит
, значит 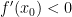 на интервале
на интервале 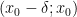 и
и 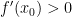 на интервале
на интервале  .
.
Таким образом функция убывает на интервале
и возрастает на интервале
по первому достаточному условию экстремума функция в точке
имеет минимум.
Аналогично доказывается второй случай теоремы.
Замечания: Если 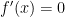 и
и  , то функция
, то функция 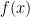 может и не иметь экстремум в точке
может и не иметь экстремум в точке 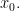
Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше 2х)
Пусть ,
и
,
Тогда:
- Если
(т.е
— четное), то
— точка экстремума:
- если
, то
— точка локального максимума;
- если
, то
— точка локального минимума;
- если
- Если
(т.е
— нечетное), то
— не является точкой экстремума.
Доказательство: Воспользуемся формулой Тейлора в окрестности точки  с остатком в форме Пеано:
с остатком в форме Пеано: 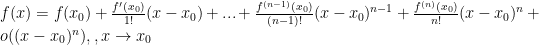 .
.
По скольку все производные до порядка включительно=0 получим:
Запишем полученное выражение в виде:
. Выражение
. Пусть
,
.

