Графическое представление энергии.

Во многих задачах рассматривается одно­мерное движение тела, потенциальная энергия которого является функцией лишь одной переменной (например, координаты х), т. е. П=П(x). График зависимости по­тенциальной энергии от некоторого аргу­мента называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела. 
Будем рассматривать только консерва­тивные системы, т. е. системы, в которых взаимные превращения механической энергии в другие виды отсутствуют.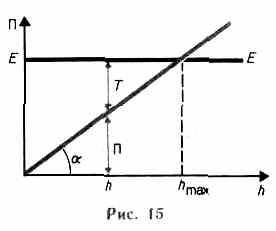 

Тогда справедлив закон сохранения энергии в форме (13.3). Рассмотрим графическое представление потенциальной энергии для тела в однородном поле тяжести и для упругодеформированного тела. 
Потенциальная энергия тела массой т, поднятого на высоту h над поверхно­стью Земли, согласно (12.7), П(h) = mgh. График данной зависимости П = П(h)— прямая линия, проходящая через начало координат (рис. 15), угол наклона которой к оси h тем больше, чем больше масса тела (так как tga = mg). 
Пусть полная энергия тела равна Е (ее график— прямая, параллельная оси h). На высоте h тело обладает потенци­альной энергией П, которая определяется отрезком вертикали, заключенным между точкой h на оси абсцисс и графиком П(h). Естественно, что кинетическая энергия Т задается ординатой между графиком П(h) и горизонтальной прямой ЕЕ. Из рис. 15 следует, что если h=hmax, то Т=0 и П = E=mghmax, т. е. потенциальная энергия становится максимальной и рав­ной полной энергии. 
Из приведенного графика можно най­ти скорость тела на высоте h: 
T=E-П, 
т. е. 
mv2/2=mghmax-mgh, откуда 
v = Ö2g(hmax-h). 
Зависимость потенциальной энергии упругой деформации П=kx2/2 от дефор­мации х имеет вид параболы (рис. 16), где график заданной полной энергии тела Е — прямая, параллельная оси

27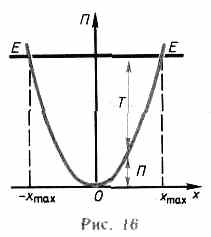

абсцисс х, а значения Т и П определя­ются так же, как на рис. 15. Из рис. 16 следует, что с возрастанием де­формации х потенциальная энергия тела возрастает, а кинетическая — уменьшает­ся. Абсцисса xmax определяет максимально возможную деформацию растяжения тела, а —xmax—максимально возможную де­формацию сжатия, тела. Если х=±xmax, то T=0 и П=E = kx2max/2, т. е. потенци­альная энергия становится максимальной и равной полной энергии. 
Из анализа графика на рис. 16 вы­текает, что при полной энергии тела, рав­ной Е, тело не может сместиться правее xmax и левее -xmax, так как кинетическая энергия не может быть отрицательной ве­личиной и, следовательно, потенциальная энергия не может быть больше полной. В таком случае говорят, что тело находит­ся в потенциальной яме с координатами 
-xmax£x£xmax. 
В общем случае потенциальная кривая может иметь довольно сложный вид, на­пример с несколькими чередующимися максимумами и минимумами (рис.17). Проанализируем эту потенциальную кривую.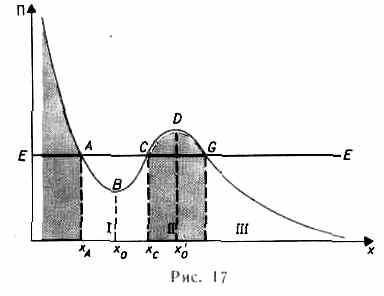 

Если Е — заданная полная энергия частицы, то частица может находиться только там, где П(х) £E, т.е. в обла­стях I и III. Переходить из области I в III и обратно частица не может, так как ей препятствует потенциальный барьер CDG, ширина которого равна интерва­лу значений х, при которых E<П, а его вы­сота определяется разностью Пmax-E. Для того чтобы частица смогла пре­одолеть потенциальный барьер, ей не­обходимо сообщить дополнительную энер­гию, равную высоте барьера или превы­шающую ее. В области 1 частица с полной энергией Е оказывается «запертой» в по­тенциальной яме ABC и совершает коле­бания между точками с координатами xaи хC. 
В точке В с координатой x0(рис. 17) потенциальная энергия частицы мини­мальна. Так как действующая на частицу сила (см. §12) Fх=-дП/дх (П — функция только одной координаты), а условие минимума потенциальной энергии дП/дх=0, то в точке В Fx = 0.При смещении частицы из положения x0(и влево, и вправо) она испытывает действие возвращающей си­лы, поэтому положение x0 является поло­жением устойчивого равновесия. Указан­ные условия выполняются и для точки х'0 (для Пmax). Однако эта точка соответству­ет положению неустойчивого равновесия, так как при смещении частицы из положе­ния х'0появляется сила, стремящаяся уда­лить ее от этого положения.