Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида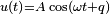 
в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний 
или её квадрата.
Дифференциальное уравнение свободных затухающих колебаний линейной системы
где s — колеблющаяся величина, описывающая тот или иной физический процесс, δ = const — коэффициент затухания, (ω0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде
(7.1) где u=u(t).
После нахождения первой и второй производных и их подстановки в (1) получим
Решение уравнения зависит от знака коэффициента перед искомой величиной. Пусть этот коэффициент положителен:
(7.2)
Тогда получим уравнение решением которого является функция u=A0cos(ωt+φ). Значит, решение уравнения (7.1) в случае малых затуханий
где 
Период затухающих колебаний с учетом формулы (7.2) равен
Если A(t) и A(t+Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение
называется декрементом затухания, а его логарифм
— логарифмическим декрементом затухания; Ne — число колебаний, совершаемых во время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.
Для характеристики колебательной системы пользуются понятием добротности, которая при малых значениях логарифмического декремента равна
Из формулы следует, что добротность пропорциональна числу колебаний Nе, совершаемых системой за время релаксации.
Для пружинного маятника массой m, совершающего малые колебания под действием упругой силы F=-kx, сила трения пропорциональна скорости, т. е.
где r — коэффициент сопротивления; знак минус указывает на противоположные направления силы трения и скорости.
При данных условиях закон движения маятника будет иметь вид
Используя формулу 
и принимая, что коэффициент затухания 
получим дифференциальное уравнение затухающих колебаний маятника:
При увеличении коэффициента затухания δ период затухающих колебаний растет и при δ = ω0 обращается в бесконечность, т. е. движение перестает быть периодическим. В данном случае колеблющаяся величина асимптотически приближается к нулю, когда t→∞. Процесс не будет колебательным. Он называется апериодическим.
