1) П. т.- предельная теорема теории вероятностей, являющаяся частным случаем больших чисел закона. П. т. обобщает Бернулли теоремуна случай независимых испытаний, вероятность появления в к-рых нек-рого события зависит от номера испытаний (т. н. схема Пуассона). Формулировка П. т. такова: если в последовательности независимых испытаний событие Анаступает с вероятностями pk, зависящими от номера испытания k, k=1,2, . . ., mn/n - частота Ав первых писпытаниях, то при любом e>0 вероятность неравенства
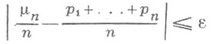
будет стремиться к 1 при  . Теорема Бернулли следует из П. т. при p1=. . .=р п. П. т. была установлена С. Пуассоном [1]. Доказательство П. т. было получено С. Пуассоном из варианта Лапласа теоремы. Простое доказательство П. т. было дано П. Л. Чебышевым (1846), к-рому также принадлежит первая общая форма закона больших чисел, включающая П. т. в качестве частного случая.
. Теорема Бернулли следует из П. т. при p1=. . .=р п. П. т. была установлена С. Пуассоном [1]. Доказательство П. т. было получено С. Пуассоном из варианта Лапласа теоремы. Простое доказательство П. т. было дано П. Л. Чебышевым (1846), к-рому также принадлежит первая общая форма закона больших чисел, включающая П. т. в качестве частного случая.
2) П. т.- предельная теорема теории вероятностей о сходимости биномиального распределения к Пуассона распределению:если Р п(m) -вероятность того, что в писпытаниях Бернулли нек-рое событие Анаступает ровно траз, причем и вероятность Ав каждом испытании равна р,то при больших значениях n и 1/р вероятность Р п (т).близка к
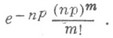
Величина l=np равна среднему значению числа наступлений А в п испытаниях, а последовательность значений 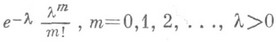 , образует распределение Пуассона. П. т. была установлена С. Пуассоном [1] для схемы испытаний, более общей, чем схема Бернулли, когда вероятности наступления события Амогут меняться от испытания к испытанию так, что
, образует распределение Пуассона. П. т. была установлена С. Пуассоном [1] для схемы испытаний, более общей, чем схема Бернулли, когда вероятности наступления события Амогут меняться от испытания к испытанию так, что 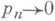 при
при  . Строгое доказательство П. т. в этом случае основано на рассмотрении схемы серий случайных величин такой, что в n-й серии случайные величины независимы и принимают значения 1 и 0 с вероятностями и р n1- р п соответственно. Более удобна форма П. т. в виде неравенства: если
. Строгое доказательство П. т. в этом случае основано на рассмотрении схемы серий случайных величин такой, что в n-й серии случайные величины независимы и принимают значения 1 и 0 с вероятностями и р n1- р п соответственно. Более удобна форма П. т. в виде неравенства: если 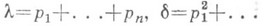
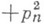 , то при
, то при 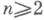
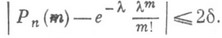
Это неравенство указывает ошибку при замене Р n (т).величиной 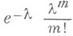 . Если p1= . . . = р п=l/п, то d =l2/n. П. т. и теорема Лапласа дают исчерпывающее представление об асимптотич. поведении биномиального распределения.
. Если p1= . . . = р п=l/п, то d =l2/n. П. т. и теорема Лапласа дают исчерпывающее представление об асимптотич. поведении биномиального распределения.
Последующие обобщения П. т. создавались в двух основных направлениях. С одной стороны, появились уточнения П. т., основанные на асимптотич. разложениях, с другой - были установлены общие условия сходимости сумм независимых случайных величин к распределению Пуассона.

