Спектр сигнала — в радиотехнике это результат разложения сигнала на более простые в базисе ортогональных функций. В качестве разложения обычно используются преобразование Фурье.Разложение сигнала в спектр применяется в анализе прохождения сигналов через электрические цепи (спектральный метод). Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал. Одним из преимуществ разложения сигнала в спектр является следующее: сигнал, проходя по цепи, претерпевает изменения (усиление, задержка, модулирование, детектирование, изменение фазы, ограничение и т. д.). Токи и напряжения в цепи под действием сигнала описываютсядифференциальными уравнениями, соответствующими элементам цепи и способу их соединения. Линейные цепи описываются линейными дифференциальными уравнениями, причём для линейных цепей верен принцип суперпозиции: действие на систему сложного сигнала, который состоит из суммы простых сигналов, равно сумме действий от каждого составляющего сигнала в отдельности. Это позволяет при известной реакции системы на какой-либо простой сигнал, например, на синусоидальное колебание с определённой частотой, определить реакцию системы на любой сложный сигнал, разложив его в ряд по синусоидальным колебаниям.
Ряд Фурье — представление произвольной функции  с периодом
с периодом  в виде ряда
в виде ряда

Этот ряд может быть также записан в виде

где
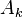 — амплитуда
— амплитуда  -го гармонического колебания,
-го гармонического колебания,
 — круговая частота гармонического колебания,
— круговая частота гармонического колебания,
 — начальная фаза
— начальная фаза  -го колебания,
-го колебания,
 —
—  -я комплексная амплитуда
-я комплексная амплитуда
В более общем виде рядом Фурье элемента гильбертова пространства называется разложение этого элемента по ортогональному базису.
Тригонометрическим рядом Фурье функции ![f\in L_2([-\pi,\pi])](http://upload.wikimedia.org/math/3/6/1/3619025a9e33eaa95a17b18dc1d1256c.png) называют функциональный ряд вида
называют функциональный ряд вида
|
|
(1) |
где

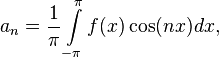

Числа 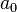 ,
,  и
и 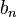 (
( ) называются коэффициентами Фурье функции
) называются коэффициентами Фурье функции  . Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию
. Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию ![f\in L_2([0,2\pi])](http://upload.wikimedia.org/math/a/4/7/a47d1c775fa95862b8751ccfa3b59eef.png) в виде ряда (1), и нам надо определить неизвестные коэффициенты
в виде ряда (1), и нам надо определить неизвестные коэффициенты 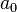 ,
,  и
и 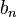 . Если умножить правую часть (1) на
. Если умножить правую часть (1) на  и проинтегрировать по промежутку
и проинтегрировать по промежутку ![[-\pi,\pi]](http://upload.wikimedia.org/math/9/1/1/911bebeafbf3d4845e122edfc4f667f8.png) , благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент
, благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент  . Аналогично для
. Аналогично для 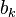
Ряд (1) сходится к функции  в пространстве
в пространстве ![L_2([-\pi,\pi])](http://upload.wikimedia.org/math/6/1/2/612a9aa246d8ab124cc4a6d5096cefaa.png) . Иными словами, если обозначить через
. Иными словами, если обозначить через  частичные суммы ряда (1):
частичные суммы ряда (1):
 ,
,
то их среднеквадратичное отклонение от функции  будет стремиться к нулю:
будет стремиться к нулю:
 .
.
Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно.
Часто при работе с рядами Фурье бывает удобнее в качестве базиса использовать вместо синусов и косинусов экспоненты мнимого аргумента. Мы рассматриваем пространство ![L^2([-\pi,\pi],\mathbb{C})](http://upload.wikimedia.org/math/0/a/d/0ad7272106ab5394e85b393bf052d8d3.png) комплекснозначных функций со скалярным произведением
комплекснозначных функций со скалярным произведением
 .
.
Мы также рассматриваем систему функций
 .
.
Как и прежде, эти функции являются попарно ортогональными и образуют полную систему, и, таким образом, любая функция ![f\in L^2([-\pi,\pi],\mathbb{C})](http://upload.wikimedia.org/math/b/0/b/b0bb7e2d24447b65c09137608c201cea.png) может быть разложена по ним в ряд Фурье:
может быть разложена по ним в ряд Фурье:
 ,
,
где ряд в правой части сходится к  по норме в
по норме в ![f\in L^2([-\pi,\pi],\mathbb{C})](http://upload.wikimedia.org/math/b/0/b/b0bb7e2d24447b65c09137608c201cea.png) . Здесь
. Здесь
 .
.
Коэффициенты :  связаны с классическими коэффициентами Фурье по следующим формулам:
связаны с классическими коэффициентами Фурье по следующим формулам:

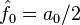



- Комплексная функция вещественной переменной раскладывается в такой же ряд Фурье по мнимым экспонентам, как и вещественная, но, в отличие от последней, для её разложения
 и
и  не будут, вообще говоря, комплексно сопряженными.
не будут, вообще говоря, комплексно сопряженными.


