1.5.1. Таблица распределения и функция распределения системы
Во многих практических задачах результат опыта описывается не одной, а двумя или более случайными величинами. В случае двух случайных величин говорят о системе двух случайных величин (X, Y) (илидвумерной случайной величине (X,Y)).
Геометрически систему двух случайных величин (X,Y) можно интерпретировать как случайную точку на плоскости.
Ограничимся рассмотрением двумерных случайных величин, принимающих конечное множество значений. Закон распределения системы (X,Y) двух дискретных случайных величин в случае конечного числа значений можно задать формулой
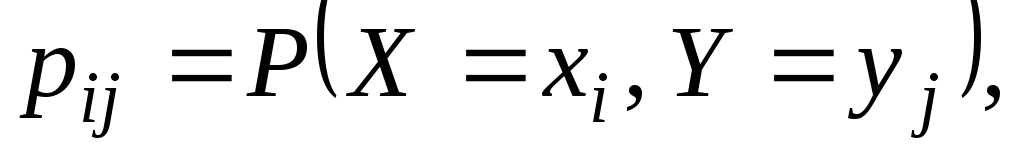 i= 1 …,n,j= 1, …,m(1.55)
i= 1 …,n,j= 1, …,m(1.55)
или с помощью таблицы с двойным ходом
|
Y X |
y1 |
y2 |
… |
ym |
|
x1 |
p11 |
p12 |
… |
p1m |
|
x2 |
p21 |
p22 |
… |
p2m |
|
. . . |
. . . |
. . . |
. . . |
. . . |
|
xn |
pn1 |
pn2 |
… |
pnm |
(1.56)
где 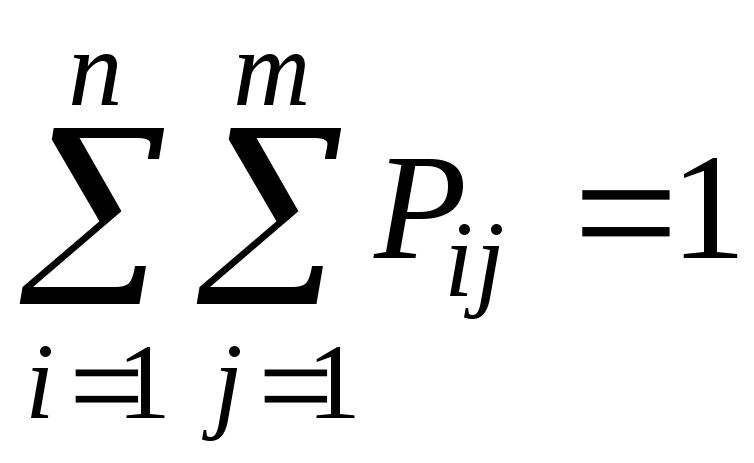 .
.
При этом
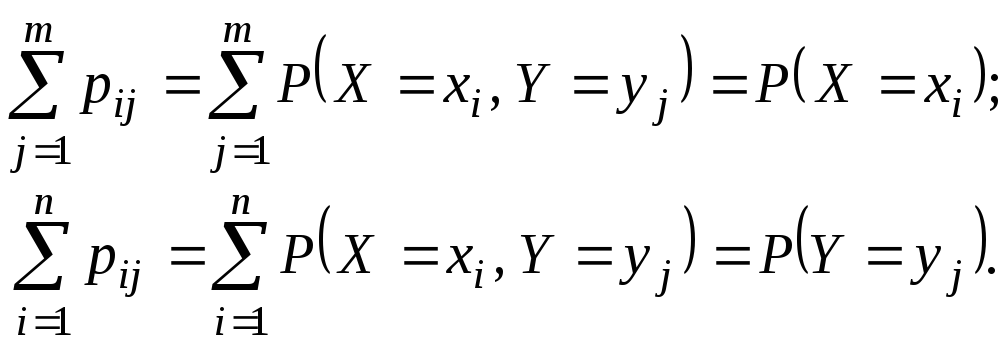 (1.57)
(1.57)
Функцией распределения системы СВ (X,Y) называется функцияF(x,y), которая для любых действительных чиселxиyравна вероятности совместного появления двух событий (X<x) и (Y<y), т. е.
F(x,y) =P(X<x,Y<y), (1.58)
где событие (X<x,Y<y) означает произведение событий (X<x) и (Y<y).
Геометрически каждое значение функции F(x,y) определяет вероятность попадания случайной точки (X,Y) в заштрихованной прямой уголRx,y(квадрант) с вершиной в точке (x,y)
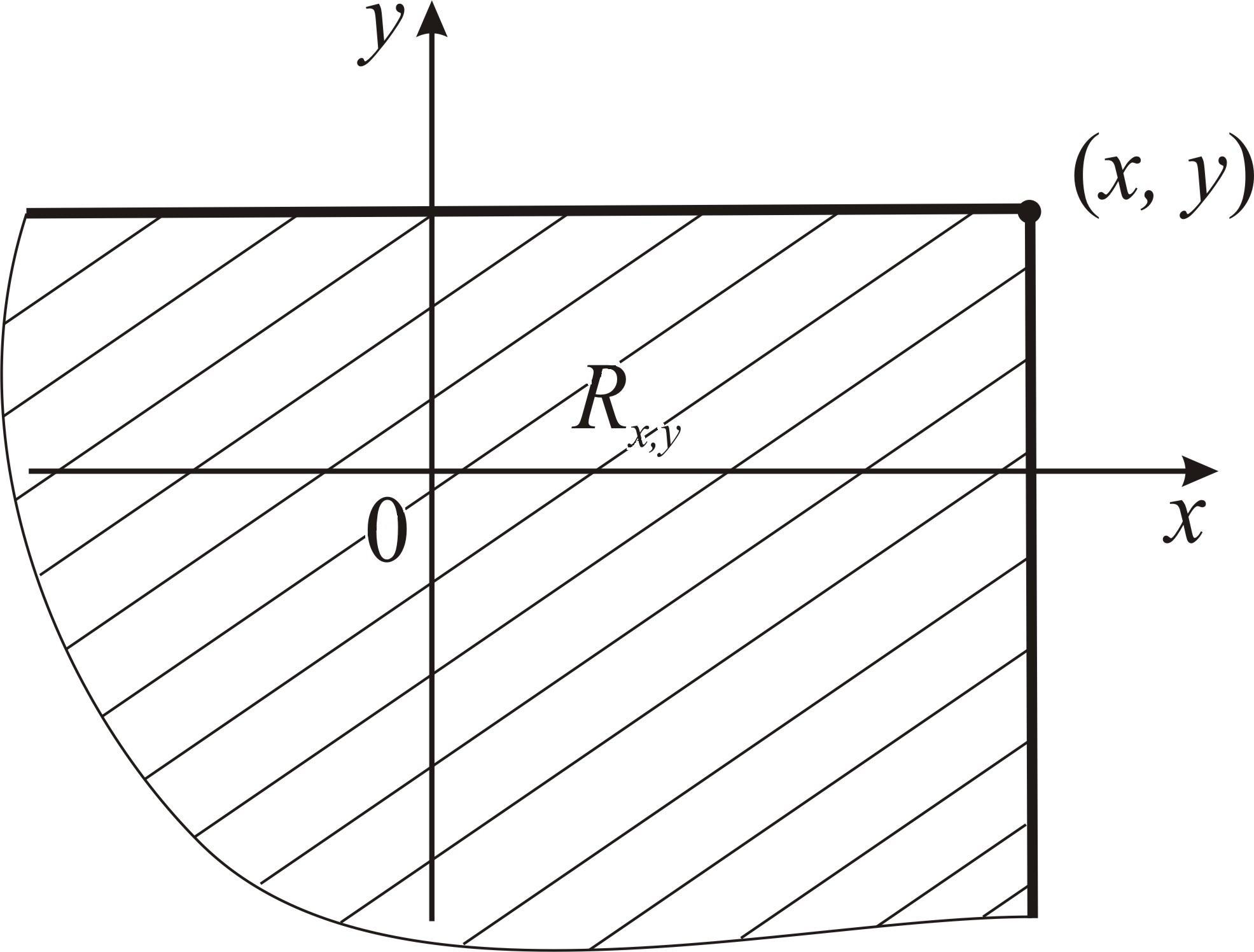
Рис. 4
Вероятность попадания случайной точки (X,Y) в прямоугольникDсо сторонами, параллельными координатным осям, находится по формуле:
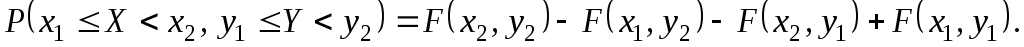 (1.59)
(1.59)
1.5.2. Свойства двумерной функции распределения
1. 0 ≤ F(x,y) ≤ 1;
2. F(x,y) не убывает по каждому из своих аргументов (при фиксированном другом аргументе):F(x2,y) ≥F(x1,y) приx2>x1;
F(x,y2) ≥F(x,y1) приy2>y1.
3. F(x,y) непрерывна слева по каждому из своих аргументов;
4. F(x, –) =F(–,y) =F(–, –) = 0, где, например,F(x, –) означает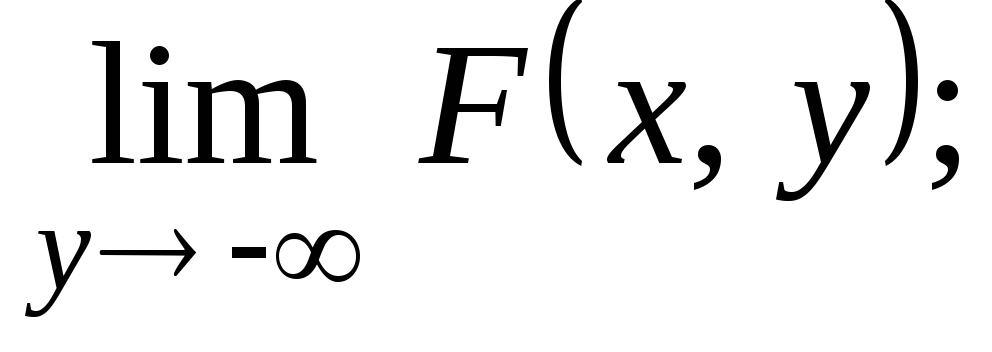
5. F(+, +) = 1;
6. F(x, +) =F1(x) =FX(x),F(+,y) =F2(y) =FY(y), гдеF1(x) иF2(y) – функции распределения СВXиYсоответственно.
Значение F(x,y) функции распределения в случае системы (X,Y) двух дискретных СВ находится суммированием всех вероятностейpijс индексамиi,jдля которыхxi<x,yj<y, т. е.
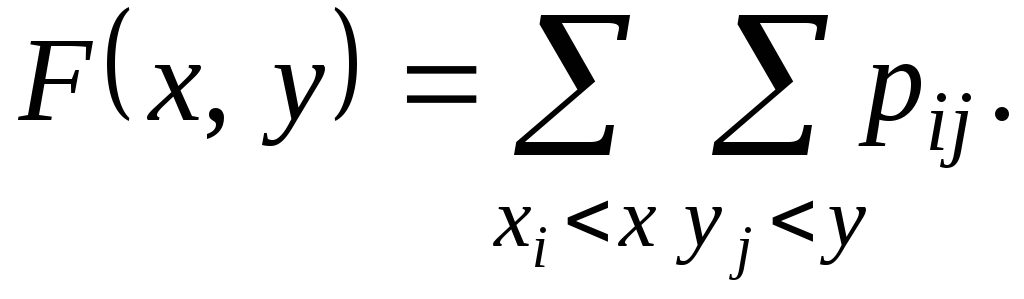 (1.60)
(1.60)
1.5.3. Независимые случайные величины
Случайные величины X и Y называются независимыми, если независимыми являются события (X < x) и (Y < y) для любых действительных чисел x и y. В противном случае случайные величины называются зависимыми.
Из определения независимости СВ ХиYследует равенство, которое можно положить в основу равносильного определения:
F(x,y) =F1(x)F2(y). (1.61)
В случае системы двух дискретных случайных величин (X,Y) необходимым и достаточным условием их независимости является равенство
P(X = xi, Y = yj) = P(X = xi) P(Y = yj), (1.62)
выполняющееся для любых i= 1, …,n,j= 1, …,m.

