Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y:
Z = j(X, Y).
Далее на примерах будет показано, как найти распределение функции Z = X + Y по известным распределениям слагаемых. Такая задача часто встречается на практике. Например, если X – погрешность показаний измерительного прибора (распределена нормально), Y – погрешность округления показаний до ближайшего деления шкалы (распределена равномерно), то возникает задача – найти закон распределения суммы погрешностей Z = X + Y.
1. Пусть X и Y – дискретные независимые случайные величины. Для того чтобы составить закон распределения функции Z = X + Y, надо найти все возможные значения Z и их вероятности.
Пример 1. Дискретные независимые случайные величины заданы распределениями:
| X | Y | |||||
| p | 0,4 | 0,6 | p | 0,2 | 0,8 |
Составить распределение случайной величины Z = X + Y.
Решение. Возможные значения Z есть суммы каждого возможного значения X со всеми возможными значениями Y:
z1 = 1 + 3 = 4; z2 = 1 + 4 = 5; z3 = 2 + 3 = 5; z4 = 2 + 4 = 6.
Найдем вероятности этих возможных значений. Для того чтобы Z = 4, достаточно, чтобы величина X приняла значение x1 = 1 и величина Y – значение у1 = 3. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равны 0,4 и 0,2.
Аргументы X и Y независимы, поэтому события X =1 и Y = 3 независимы и, следовательно, вероятность их совместного наступления (т.е. вероятность события Z = 1 + 3 = 4) по теореме умножения равна 0,4×0,2 = 0,08.
Аналогично найдем:
P(Z = 1 + 4 = 5) = 0,4×0,8 = 0,32;
Р(Z = 2 + 3 = 5) = 0,6×0,2 = 0,12;
Р(Z = 2 + 4 = 6) = 0,6×0,8 = 0,48.
Напишем искомое распределение, сложив предварительно вероятности несовместных событий Z = z2, Z = z3 (0,32 + 0,12 = 0,44):
| Z | |||
| p | 0,08 | 0,44 | 0,48 |
Контроль: 0,08 + 0,44 + 0,48 = 1.
2. Пусть X и Y – непрерывные случайные величины. Доказано: если X и Y независимы, то плотность распределения g(z) суммы Z = X + Y (при условии, что плотность хотя бы одного из аргументов задана на интервале (–¥, ¥) одной формулой) может быть найдена с помощью равенства
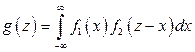 (11.12)
(11.12)
либо с помощью равносильного равенства
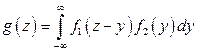 , (11.13)
, (11.13)
где f1, f2 – плотности распределения аргументов.
Если возможные значения аргументов неотрицательны, то g(z) находят по формуле
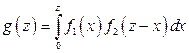 (11.14)
(11.14)
либо по равносильной формуле
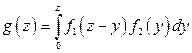 . (11.15)
. (11.15)
Определение. Плотность распределения суммы независимых случайных величин называют композицией.
Определение.Закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойством устойчивости: композиция нормальных законов также имеет нормальное распределение (математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых). Например, если X и Y – независимые случайные величины, распределенные нормально с математическими ожиданиями и дисперсиями, соответственно равными а1 = 3, а2 = 4, D1 = 1, D2 = 0,5, то композиция этих величин (т.е. плотность вероятности суммы Z = X + Y) также распределена нормально, причем математическое ожидание и дисперсия композиции соответственно равны а = 3 + 4 = 7; D = 1 +0,5 = 1,5.
Пример 2. Независимые случайные величины X и Y заданы плотностями распределений:
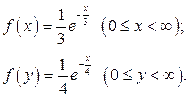
Найти композицию этих законов, т.е. плотность распределения случайной величины Z = X + Y.
Решение. Возможные значения аргументов неотрицательны, поэтому воспользуемся формулой (11.14)
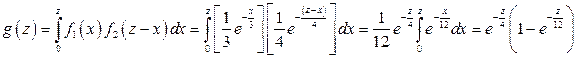 .
.
Заметим, что здесь z ³ 0, так как Z = X + Y и, по условию, возможные значения X и Y неотрицательны. Можно для контроля убедиться, что
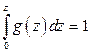 .
.
Рассмотрим некоторые распределения, связанные с нормальным, которые будут использованы при изложении математической статистики.
11.13. Распределение «хи квадрат»
Пусть Xi (i = 1, 2, ..., n) – нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее ческое отклонение – единице. Тогда сумма квадратов этих величин
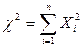 .
.
распределена по закону c2 («хи квадрат») с k = n степенями свободы; если же эти величины связаны одним линейным соотношением, например 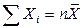 , то число степеней свободы k = n – 1.
, то число степеней свободы k = n – 1.
Плотность этого распределения
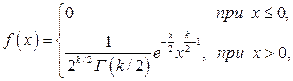 .
.
где 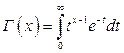 – гамма-функция; в частности,
– гамма-функция; в частности,
Г(x) = (n + 1) = n!.
Отсюда видно, что распределение «хи квадрат» определяется одним параметром – числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.

