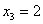Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина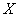 
принимает значения 
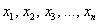с вероятностями 
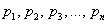соответственно. Тогда математическое ожидание 
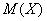данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:
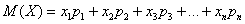
или в свёрнутом виде: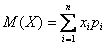
Вычислим, например, математическое ожидание случайной величины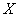 
– количества выпавших на игральном кубике очков:
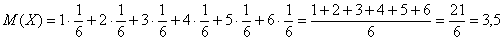очка
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру: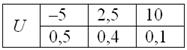
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
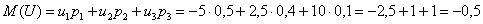, таким образом, математическое ожидание данной игры проигрышно.
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры :) Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Пример 4
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины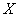 
– его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
Пример 5
Случайная величина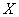 
задана своим законом распределения вероятностей: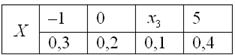
Найти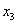 
, если известно, что 
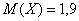. Выполнить проверку.
Есть?
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
Решения и ответы:
Пример 3. Решение: по условию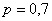 
– вероятность попадания в мишень. Тогда:
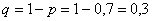– вероятность промаха.
Составим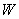 
– закон распределения попаданий при двух выстрелах:
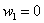– ни одного попадания. По теореме умножения вероятностей независимых событий: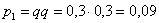
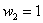– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий: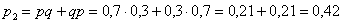
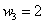– два попадания. По теореме умножения вероятностей независимых событий: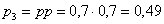
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ: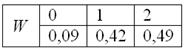 
Примечание: можно было использовать обозначения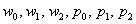 
– это не принципиально.
Пример 4. Решение: поскольку игрок выигрывает в 18 случаях из 37, то закон распределения его выигрыша имеет следующий вид: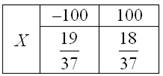
Вычислим математическое ожидание: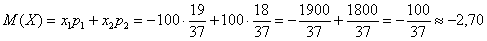
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: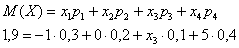
поменяем части местами и проведём упрощения: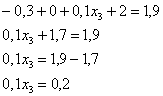
таким образом: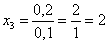
Выполним проверку: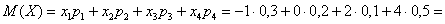
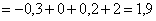, что и требовалось проверить.
Ответ: 
