Теорема 1. Если функция имеет предел в точке, то этот предел единственный.
Теорема 2. Если функция имеет предел в точке, то она ограничена в некоторой проколотой окрестности этой точки.
Теорема 3. Если функция 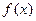 имеет предел
имеет предел 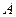 в точке
в точке 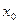 , то существует проколотая окрестность точки, в которой функция
, то существует проколотая окрестность точки, в которой функция 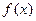 имеет знак, совпадающий со знаком предела
имеет знак, совпадающий со знаком предела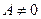 .
.
Теорема 4. Если 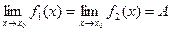 и в некоторой проколотой окрестности точки
и в некоторой проколотой окрестности точки 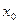 имеют место неравенства
имеют место неравенства 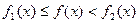 , то
, то 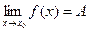 .
.
Теорема 5. Пусть функции 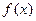 и
и 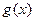 имеют предел в точке
имеют предел в точке 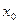 . Тогда справедливы формулы:
. Тогда справедливы формулы:
1)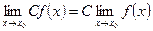 , где С=const;
, где С=const;
2) 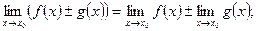
3) 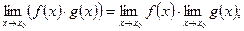
4) 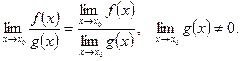
Замечание 1. Формулы суммы и произведения обобщаются на любое конечное число множителей. Если использовать их для бесконечного количества множителей, то может возникнуть ошибка.
Замечание 2. Если в результате применения формул 1) – 4) приходим к выражениям типа
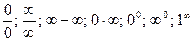
которые называют неопределенностями, то следует вначале устранить неопределенность, сделав тождественные преобразования.
Теоремы о пределах о свойствах функций, имеющих конечные пределы
ТЕОРЕМА (о единственности предела)
Пусть произвольная функция  определена в некоторой
определена в некоторой
окрестности точки  ,
,  .
.
Тогда если функция  при
при  имеет конечный предел, то он единственный, т.е.
имеет конечный предел, то он единственный, т.е.
 ;
;  .
.
Доказательство методом от противного
Предположим  . Тогда
. Тогда
 ,
,
в частности и при  ;
;
 ,
,
в частности и при  .
.
Отсюда на  имеем
имеем 
 – неверное числовое неравенство.
– неверное числовое неравенство.
Вывод: предположение о существовании не единственного
предела – ложное. Теорема доказана.
Частный случай (для последовательности)
 .
.
 Если предположить наличие двух различных пределов, то можно указать непересекающиеся окрест-ности этих пределов, в которые должны попадать одновременно ВСЕ
Если предположить наличие двух различных пределов, то можно указать непересекающиеся окрест-ности этих пределов, в которые должны попадать одновременно ВСЕ
члены последовательности, начиная с некоторого.
ТЕОРЕМА (о локальной ограниченности функции, имеющей
при  конечный предел)
конечный предел)
 :
:  ,
,
т.е. если функция при  имеет конечный предел, то существует окрестность точки
имеет конечный предел, то существует окрестность точки  , на которой множество значений функции
, на которой множество значений функции  есть ограниченное числовое множество.
есть ограниченное числовое множество.
Доказательство. Поскольку  к.ч., то для любого
к.ч., то для любого  , в том числе для
, в том числе для  , существует
, существует  так, что для
так, что для 
 , т.е.
, т.е.  , где
, где 
 или
или  .
.
Заметим, что обратное утверждение неверно, т.е. если функция  локально ограничена на
локально ограничена на  , то необязательно существует
, то необязательно существует  и равен конечному значению.
и равен конечному значению.
Контрпример. Функция  имеет множество значений
имеет множество значений  – ограниченное множество в любой окрестности точки
– ограниченное множество в любой окрестности точки  , но
, но  не существует.
не существует.
Заметим, что функция, имеющая в точке конечный предел, а значит, локально ограниченная в окрестности этой точки, может быть неограниченной на своей области существования. Например,  ,
,  для
для  .
.
Функция  бесконечно большая при
бесконечно большая при  является неограниченной в любой окрестности
является неограниченной в любой окрестности  . Обратное неверно, т.е. неограниченная в
. Обратное неверно, т.е. неограниченная в  функция
функция  не обязательно бесконечно большая при
не обязательно бесконечно большая при  . Например,
. Например, 
 .
.
Частный случай (для последовательности):
всякая сходящаяся последовательность является ограниченной, т.е.

Контрпример.  – ограниченная последователь-ность, но не является сходящейся, поскольку ее подпосле-довательности
– ограниченная последователь-ность, но не является сходящейся, поскольку ее подпосле-довательности  и
и  сходятся к несовпадающим пределам.
сходятся к несовпадающим пределам.
Итак, теорема о локальной ограниченности является "односторонней" теоремой и выражает НЕОБХОДИМОЕ условие существования конечного предела функции (и последовательности).
Следующая серия утверждений описывает связь между соотношениями для функций и их пределов.
ТЕОРЕМА (о переходе к пределу в равенстве)
Если  на
на  и существует
и существует  , то существует
, то существует  и
и  .
.
ПРИМЕР. Поскольку  для
для  и
и  , то
, то  .
.
ТЕОРЕМА (о переходе к пределу в неравенстве)
Если  или
или  на
на  и существуют
и существуют  – к.ч. и
– к.ч. и  – к.ч., то
– к.ч., то  .
.
Доказательство можно провести методом от противного.
Рекомендуем провести самостоятельно.
ТЕОРЕМА (о перенесении неравенства между пределами на функции)
Если существуют пределы  и
и  и выполняется неравенство
и выполняется неравенство  , то существует окрестность
, то существует окрестность  ,
,
на которой  .
.
Доказательство. Имеем
 ,
,
в частности, при 
 :
: 
 , т.е.
, т.е.  . Аналогично
. Аналогично
 ,
,
в частности, при 

 , т.е.
, т.е.  или
или  .
.
Поскольку при 
 , то на пересечении окрестностей
, то на пересечении окрестностей  имеем
имеем  , т.е. указали окрестность
, т.е. указали окрестность  , на которой характер неравенства между пределами переносится на функции.
, на которой характер неравенства между пределами переносится на функции.
Следствие. Если  – конечное число и
– конечное число и  , то можно указать окрестность
, то можно указать окрестность  , на которой
, на которой  .
.
ТЕОРЕМА (о пределе промежуточной функции)
Если  на
на  и существуют
и существуют  и
и  и их значения конечны и равны, то существует предел промежуточной функции
и их значения конечны и равны, то существует предел промежуточной функции  и его значение совпадает со значением пределов оценивающих слева и справа функций.
и его значение совпадает со значением пределов оценивающих слева и справа функций.
Доказательство рекомендуем построить самостоятельно,
используя определение предела по Коши для функций  и
и  при
при  .
.
ТЕОРЕМА (об арифметике функций, имеющих конечный предел в одной и той же точке)
Пусть функции  и
и  при
при  имеют конечные пределы, т.е.
имеют конечные пределы, т.е.  ,
,  ,
,  и
и  – конечные числа.
– конечные числа.
Тогда при  имеет конечный предел каждая из функций:
имеет конечный предел каждая из функций:
1)  ; 2)
; 2)  ; 3)
; 3)  (при
(при  ).
).
Доказательство. 1. Операция сложения функций определяется поточечно. Утверждение верно для произвольного конечного
множества функции. Здесь рассматривается сумма двух функций.
Имеем  , т.е. для всякого
, т.е. для всякого  (в частности, для
(в частности, для  ) существует
) существует  так, что
так, что 
 .
.
Аналогично ( )
) (
( ,
,
 ).
).
Рассмотрим и оценим: 

на  .
.
Итак, 
 , т.е. по определению предела
, т.е. по определению предела  – конечное
– конечное
число, причем предел СУММЫ функций равен СУММЕ пределов слагаемых функций, если предел каждой слагаемой функции – конечное число.
Заметим, что обратное утверждение неверно, т.е. существование конечного предела суммы функций не определяет существование предела каждого слагаемого.
Контрпример. Пусть  ,
,  , тогда
, тогда  . Но сумма функций может быть представлена слагаемыми (неоднозначно), например в виде
. Но сумма функций может быть представлена слагаемыми (неоднозначно), например в виде  и
и  , и пределы слагаемых при
, и пределы слагаемых при  не являются конечными числами (не существуют).
не являются конечными числами (не существуют).
2. Представим 
 .
.
Имеем  – конечное число, поэтому
– конечное число, поэтому  – локально ограничена, т.е.
– локально ограничена, т.е.  .
.
Исходя из определения конечного предела при  имеем также
имеем также 
 .
.
При  оценивать второе слагаемое в представлении не
оценивать второе слагаемое в представлении не
требуется. При  расшифруем
расшифруем 
 .
.
Получаем на окрестности 
 , и по определению предела
, и по определению предела
 .
.
Итак, предел ПРОИЗВЕДЕНИЯ функций равен ПРОИЗВЕДЕНИЮ пределов функций, если предел каждой функции в произведении – конечное число.
Обратное утверждение неверно.
Контрпример. Пусть  ,
,  , тогда
, тогда  . Но произведение функций может быть представлено сомножителями неоднозначно, например
. Но произведение функций может быть представлено сомножителями неоднозначно, например  и
и  , и тогда предел сомножителя
, и тогда предел сомножителя  не является конечным.
не является конечным.

