Пусть функция 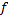 , определённая на отрезке
, определённая на отрезке  , ограничена на этом отрезке и пусть
, ограничена на этом отрезке и пусть 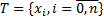 - разбиение отрезка
- разбиение отрезка  ,
, 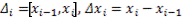 (i=1,n). Обозначим
(i=1,n). Обозначим
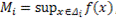 ,
,  ,
,
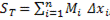 ,
, 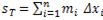 . (5)
. (5)
Назовём 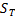 и
и  соответственно верхней и нижней суммами Дарбу для функции
соответственно верхней и нижней суммами Дарбу для функции 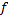 при заданном разбиении
при заданном разбиении 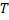 отрезка
отрезка  . Заметим, что эти суммы не зависят от выборки
. Заметим, что эти суммы не зависят от выборки 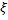 . Рассмотрим свойства сумм Дарбу.
. Рассмотрим свойства сумм Дарбу.
С в о й с т в о 1. Для любой выборки 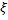 справедливы неравенства
справедливы неравенства
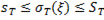 . (6)
. (6)
○ Так как для любого 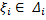 , выполняются неравенства
, выполняются неравенства
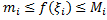
то
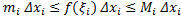
Складывая эти неравенства, получаем
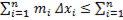
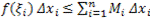 . (7)
. (7)
Согласно определению сумм Дарбу и интегральной суммы 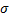 утверждения (7) и (6) равносильны. ●
утверждения (7) и (6) равносильны. ●
С в о й с т в о 2. Справедливы равенства
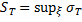 , (8)
, (8)
 . (9)
. (9)
○ Докажем утверждение (8). Согласно определению точной верхней грани нужно доказать, что выполняются следующие условия:
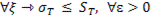
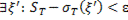 .
.
Первое из этих условий выполняется в силу (6). Докажем второе условие.
Так как 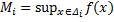 , то по определению точной верхней грани
, то по определению точной верхней грани
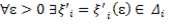 :
: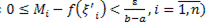 .
.
Умножая -е неравенство на 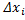 и складывая все полученные неравенства, находим
и складывая все полученные неравенства, находим
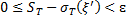 ,
,
Где 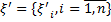 - выборка. Итак, утверждение (8) доказано. Аналогично доказывается, что справедливо и утверждение (9).●
- выборка. Итак, утверждение (8) доказано. Аналогично доказывается, что справедливо и утверждение (9).●
Следующее свойство сумм Дарбу связано с ещё одним понятием для разбиений. Назовём разбиение 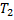 продолжением (измельчением) разбиения
продолжением (измельчением) разбиения 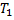 , если каждая точка разбиения
, если каждая точка разбиения 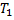 является точкой разбиения
является точкой разбиения 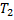 . Иначе говоря, Разбиение
. Иначе говоря, Разбиение 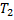 либо совпадает с разбиением
либо совпадает с разбиением 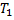 , либо получено из
, либо получено из 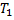 добавлением по крайней мере одной новой точки.
добавлением по крайней мере одной новой точки.
С в о й с т в о 3. Если разбиение 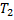 - продолжение разбиения
- продолжение разбиения 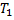 , то
, то
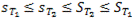 (10)
(10)
т.е. при измельчении разбиения нижняя сумма Дарбу не уменьшается, а верхняя не увеличивается.
○ Для доказательства неравенств (10) достаточно рассмотреть случай, когда разбиение 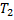 получается из разбиения
получается из разбиения 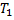 добавлением только одной точки
добавлением только одной точки 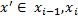 . пусть
. пусть 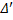 и
и 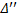 - отрезки, на которые точка
- отрезки, на которые точка 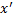 разбивает отрезок
разбивает отрезок 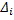 , а
, а 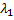 и
и 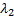 - длины этих отрезков; тогда
- длины этих отрезков; тогда 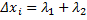 . Обозначим
. Обозначим 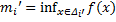 ,
, 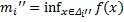 . Очевидно, что
. Очевидно, что  ,
,  .
.
В суммах 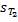 и
и 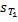 равны все соответствующие слагаемые, за исключением тех, которые связаны с отрезком
равны все соответствующие слагаемые, за исключением тех, которые связаны с отрезком 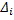 . Поэтому
. Поэтому
 +
+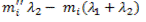 ,
,
где  ,
,  . Следовательно,
. Следовательно,
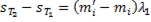 +
+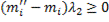 , т.е.
, т.е. 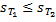 .
.
Аналогично доказывается неравенство 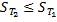 . Отсюда, используя неравенство
. Отсюда, используя неравенство  (см.(6)), получаем цепочку неравенств (10). ●
(см.(6)), получаем цепочку неравенств (10). ●
С в о й с т в о 4. Для любых разбиений 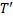 и
и  справедливо неравенство
справедливо неравенство
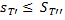 (11)
(11)
○ Пусть разбиение 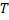 является продолжением как разбиения
является продолжением как разбиения 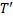 , так и разбиения
, так и разбиения  (в качестве
(в качестве 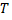 можно взять
можно взять 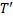 и добавить к нему те точки разбиения
и добавить к нему те точки разбиения  , которые не входят в
, которые не входят в 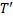 ).
).
Из неравенств (10) при 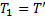 ,
, 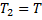 получаем
получаем
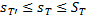 .
.
Полагая в (10) 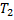 =
= 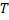 и
и 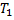 =
= , находим
, находим
 .
.
Объединяя полученные неравенства, имеем
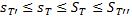 ,
,
Откуда следует неравенство (11).●
С в о й с т в о 5. Существуют числа
 ,
,
Удовлетворяющие для любых разбиений 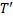 и
и 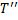 отрезка
отрезка  условию
условию
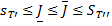 (12)
(12)
Эти числа называют соответственно нижним и верхним интегралами Дарбу от функции 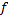 на отрезке
на отрезке  .
.
○ Из неравенства (11) по теореме об отделимости числовых множеств следует, что существует 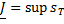 и
и 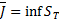 (супремум и инфимум по всевозможным разбиениям отрезка
(супремум и инфимум по всевозможным разбиениям отрезка  и для любых разбиений
и для любых разбиений 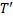 и
и  выполняется неравенство (12).●
выполняется неравенство (12).●
В заключение отметим, что свойства 1-5 справедливы для любой ограниченной на отрезке  функции.
функции.
Критерий интегрируемости функции.
Т е о р е м а 2. Для того, чтобы функция 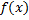 , определённая на отрезке
, определённая на отрезке  , была интегрируема на этом отрезке, необходимо и достаточно, чтобы эта функция была ограничена и удовлетворяла условию
, была интегрируема на этом отрезке, необходимо и достаточно, чтобы эта функция была ограничена и удовлетворяла условию
 <
<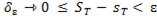 . (13)
. (13)
○ Н е о б х о д и м о с т ь. Пусть функция 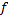 интегрируема на отрезке
интегрируема на отрезке  . Тогда она ограничена (теорема 1) и в силу определения интеграла
. Тогда она ограничена (теорема 1) и в силу определения интеграла
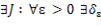 >0:
>0: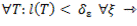
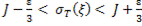 .
.
Таким образом, при каждом разбиении 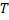 отрезка
отрезка  , мелкость которого удовлетворяет условию
, мелкость которого удовлетворяет условию 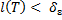 , неравенство
, неравенство
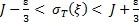 (14)
(14)
Выполняется при любой выборке 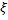 . Поэтому из левого неравенства (14) и равенства (9) следует, что
. Поэтому из левого неравенства (14) и равенства (9) следует, что
 . (15)
. (15)
Аналогично из правого неравенства (14) и равенства (8) следует, что
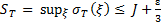 . (16)
. (16)
Из неравенств (15), (6) и (16) получаем цепочку неравенств
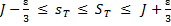 ,
,
откуда следует, что
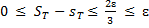 .
.
Итак, интегрируемая на отрезке функция 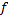 удовлетворяет условию (13).
удовлетворяет условию (13).
Д о с т а т о ч н о с т ь. Пусть функция 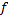 ограничена на отрезке
ограничена на отрезке  и удовлетворяет условию (13). Докажем, что функция
и удовлетворяет условию (13). Докажем, что функция 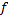 интегрируема на отрезке
интегрируема на отрезке  , т.е.
, т.е.
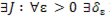 >0:
>0: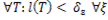
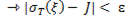 . (17)
. (17)
Воспользуемся свойством 5. Из неравенств (12) следует, что
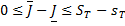 ,
,
откуда в силу (13) получаем неравенство
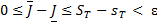 ,
,
Справедливое для любого разбиения 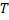 такого, что
такого, что 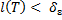 . Так как числа
. Так как числа 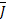 и
и 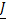 не зависят от
не зависят от 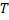 , то отсюда следует, что
, то отсюда следует, что
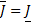 .
.
Обозначим
 (18)
(18)
И докажем, что число  есть интеграл от функции
есть интеграл от функции 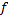 на отрезке
на отрезке  .
.
Из (12) и (18) следует, что
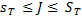 , (19)
, (19)
А из (19) и (6) в силу (13) получаем
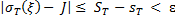 .
.
Это означает, что функция 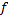 интегрируема на отрезке
интегрируема на отрезке  , а число
, а число  есть интеграл от
есть интеграл от 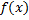 на
на  .●
.●

