Исчисление предикатов (ИП) служит тем же целям, что ИВ, но оно шире, так как наряду с высказываниями использует предикаты.
Предикат Р -это отношение. Запись aRb или a < b можно заменить обозначением Р ( a, b ). Предикат имеет место или нет в зависимости от предметных переменных a и b, от которых он зависит.
Можно пронимать предикат как функцию, принимающую как булева функция значения из множества { 0,1} , но аргументами здесь являются уже не булевы, а предметные переменные. В названии такой переменной подчеркивается её отличие от булевой, т.е. двоичной переменной. Часто (хотя и необязательно) подразумевают некоторую количественную характеристику предметной переменной, и тогда a ОM и bОM, где М - множество чисел, возможно бесконечное.
С помощью понятия предиката можно любую функцию и любое отношение свести к булевой переменной, так как Р О{ 0,1} . Например:
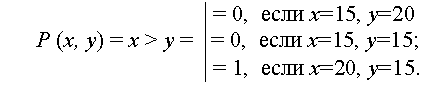
В качестве простого высказывания, т.е. в виде булевой переменной Р предикат можно включать в качестве аргумента в формулы исчисления высказываний. Благодаря этому предикат представляет обобщающую форму, позволяющую сводить рассуждения о существовании или несуществовании различных отношений к логическому высказыванию.
Рассмотрим простую задачу. Некто А хочет навестить В, но знает, что это собираются также сделать С, D и Е. А ничего не имеет против С и D по отдельности, но обоих сразу видеть не хочет. С Е он вообще не хотел бы встречаться. Известно также, что С придет к В в промежутке между пятью и шестью часами, D - в промежутке между семью и восемью часами и Е - не раньше девяти. Когда же следует приходить А? Или по-другому: когда приходить, чтобы вообще ни с кем из упомянутых визитеров не встретиться? Эту задачу каждый решит в уме на основе рассуждений, но так можно решать только простые задачи. Главный вопрос здесь - как формализовать задачу?
Обозначим количественные условия задачи в виде предикатов:
P1(t) = (5<t<6), P2 = (7<t<8), P3 = (9<t).
Теперь задача может быть описана логической функцией, которая обращается в единицу, если условия выполнены. Первый вариант условий: "не встретить Е и не встретить сразу С и D" выражается формулой:
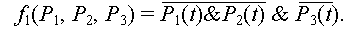
Второе условие "вообще никого не встретить" обеспечено при
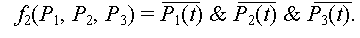
Задача решена в теоретическом плане, но для получения прикладного решения придется найти удобный алгоритм перебора значений t.
Часто предикаты используют просто для того, чтобы указать на существование некоторого отношения. Если например Р(х) = (х>15), то запись Р(х) просто заменяет выражение х>15. Нет необходимости писать Р(х) = 1, достаточно написать просто Р(х). Если же Р(х) = 0, то вместо этого пишут `Р(х).
Для замены словесных утверждений об условиях существования предиката используются кванторы.
Квантор всеобщности "х означает "все х" или "для всех х". Выражение
" хР(х), хОМ
заменяет фразу: "Для всех х, принадлежащих М, имеет место отношение Р". Можно прочитать его короче: "Для всех х из М, Р(х)". Этим словам по звучанию больше соответствовала бы запись "хОМ, Р(х), но она неверна. Квантор имеет смысл только с указанием предметной переменной. Обозначение "х -это один символ, дробить который нельзя. "хОМ -неверно, так как не ясно, что именно является элементом М. Символ квантора должен стоять непосредственно перед обозначением предиката.
Квантор существования $х означает "существует х". Запись
$хР(х)
заменяет фразу: "Существует такой х, который удовлетворяет отношение Р" или короче: "существует такой х, что Р(х)".
Квантор существования и единственности $!х означает, что имеется единственное значение предметной переменной х, которое удовлетворяет отношение Р.
Иногда знаки " и $ используют просто для сокращения записи вместо слов "все" и "существует", вне всякой связи с исчислением предикатов. В этом случае названные знаки кванторами не являются.
Мы будем использовать "х и $х именно как кванторы, т.е. знаки предикатных выражений. Как уже говорилось, символ квантора должен стоять непосредственно перед обозначением предиката, а сам предикат считается областью действия квантора. Если область действия квантора должна распространяться на несколько предикатов, то её выделяют скобками, например
$ х ( Р1 (х, у ), Р2 (х, z )).
Добавление квантора или, как говорят навешивание квантора меняет смысл предикатной формулы. Пусть, например хО{ 0,1,2,...50} , P(x) = (x >15). Тогда Р(х) может быть истинным или ложным высказыванием в зависимости от величины х, которая является свободной предметной переменной. Зато "хР(х) -заведомо ложно, а $хР(х) -всегда истинно, независимо от величины х. После навешивания квантора предметная переменная становится связанной. Она по-прежнему может меняться, но это уже не влияет на истинность выражения. Следовательно, предикат, в котором все предметные переменные связаны кванторами, превращается в логическое высказывание с фиксированной, не зависящей от предметных переменных истинностью.
Навешивание одного квантора на предикатную формулу связывает только одну предметную переменную, уменьшая на единицу число оставшихся свободными переменных. Примем хОM, yОM, M = { 0,1,2,...50} , P(x, у) = (x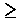
y).
Меняя кванторы местами, мы меняем смысл высказывания. Поэтому можно менять местами лишь одинаковые кванторы. Оба последние высказывания истинны, так как множество М с предикатом Р образует линейно упорядоченное множество, в котором непременно имеются как максимум, так и минимум.
Предикатные выражения могут подставляться в логические формулы, как при наличии свободных предметных переменных, так и при полной квантификации, когда все предметные переменные связаны. Следовательно, в любом случае над выражениями с кванторами приходится производить эквивалентные преобразования. Вот некоторые важнейшие из них:
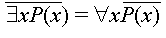
"нет такого х, что Р(х)" = "для всех х Р(х) не имеет места";
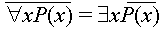
"не для всх х действительно Р(х)" = "есть такой х , что Р(х) не имеет места".
Квантор всеобщности дистрибутивен относительно конъюнкции:
"х(Р1(х)&P2(x)) = "xP1(x)&"хP2(x)
Квантор существования дистрибутивен относительно дизъюнкции
$х(Р1(х)U Р2(х)) = $хР1(х) U $хР2(х).
Формула может содержать некоторую функцию f, не зависящую от переменной х. Тогда эту функцию можно вынести из области действия квантора, связывающего х:
"х(Р(х)&f) = "xP(x)&f,
что вытекает из дистрибутивности "х относительно &. Но можно доказать и такое неочевидное преобразование
"х(Р(х)Ъf) = "хР(x)Ъf
Доказательство. Преобразование
"хР1(х)Ъ"хР2(х) = "х(Р1(х)ЪР2(х))
не эквивалентно, так как левая часть представляет более сильное утверждение: либо для всех х существует Р1, либо для всех х - Р2. Правая часть мягче потому, что для каждого х требуется существование хотя бы одного из предикатов. Если левая часть истинна, то правая тоже истинна, хотя обратное утверждение неверно. Так происходит, если оба предиката: Р1 и Р2 зависят от х. Если же один из предикатов, например Р2 от х не зависит, то утверждения в левой и правой частях последнего равенства равносильны.
Аналогично доказываются преобразования
$х(Р(х)&f) = $хР(х)&f,
$х(Р(х)Ъf) = $xP(x)Ъf.
Различают два вида исчисления предикатов: общее ИП, которое допускает наряду с обычными кванторами по предметным переменным также кванторы по предикатам "Р(Р(х)), $Р(Р(х)) и т.п. и узкое ИП, где кванторы последнего вида недопустимы. Общее ИП весьма сложно и имеет мало приложений. Нижесказанное касается только узкого ИП.
Как и всякое другое исчисление ИП задается формально:
- Задается алфавит ИП. В нем содержатся: символы предметных переменных х1, х2,...; констант с1, с2,...; отношений Р1, Р2,...; пропозициональных (логических) связок Ъ, &, `x, ® ; кванторов "х и $х, скобки и запятые. Кроме того, в алфавите содержатся пропозициональные буквы (логические высказывания) А1, А2,..., которые для общности можно считать просто 0-местными предикатами;
- Рекурсией определяется бесконечное множество формул:
(Ф1 Ъ Ф2), (Ф11&Ф2), (Ф1). (Ф1® Ф2);
- предметные переменные х и константы с есть термы t;
- если Р -предикатная буква, а t1, t2,...tn - термы, то Р(t1, t2,...tn) -формула;
- если Ф1 и Ф2 - формулы, то формулами будут также:
- если Ф(х) -формула (содержащая свободные вхождения переменной х), то "хФ(х) и $хФ(х) -тоже формулы (со связанной переменной х);
- Определяются аксиомы ИП. В их числе должны быть указаны аксиомы какого-нибудь одного ИВ и две общие предикатные аксиомы:
"хФ(х)® Ф(у) и Ф(у)® $хФ(х).
Смысл первой из них: если Ф(х) истинно для любого х, то оно должно быть истинным и при замене х на некоторую переменную у (из того же множества М). Смысл второй аксиомы: Если Ф(у) истинно для какого-нибудь у, то существует хотя бы один х, такой. что Ф(х) истинно.
Предикатные аксиомы применимы с двумя условиями:
- Ф(х) должна содержать свободные вхождения х, причем ни одно из них не должно находиться в области действия квантора по у. То же самое должно обеспечиваться для Ф(у);
- при построении Ф(у) из Ф(х) буквой у заменяются сразу все свободные вхождения х в формулу.
- Указываются правила вывода. К обычному правилу modus ponens (или к другим правилам ИВ) добавляются ещё два: так называемые правила "-введения и $ -введения
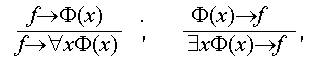
где f -формула, не содержащая свободных вхождений х.
Как уже говорилось, над формулами ИП можно производить эквивалентные преобразования. К восьми уже описанным преобразованиям добавим преобразования для импликации:
"х(Ф(х)® f) = "хФ(х)® f,
$х(Ф(х)® f) = $хФ(х)® f,
"х(f® Ф(х)) = f® "хФ(х),
$х(f® Ф(х)) = f® $хФ(х).
С помощью этих и других, более сложных преобразований с введением новых предметных переменных стараются все кванторы вынести вперед или, что то же самое, спустить все логические операции в область действия кванторов. В итоге стремятся получить т. называемую предваренную или пренексную формулу вида
$v"х"у$zФ( v, х, у, z ),
где выражение Ф не содержит кванторов. Такая формула может быть в принципе получена из любой первоначально заданной формулы ИП.
ИП в описанном виде называется чистым ИП, которое нельзя использовать для прикладных задач, так как смысл предикатов не определен. Прикладное ИП в отличие от чистого, содержит ещё специальные аксиомы о свойствах конкретных отношений, которыми оперирует данное ИП. Когда прикладное ИП получают из узкого чистого ИП (кванторы только по переменным), полученное исчисление называется теорией первого порядка. Из общего ИП получаются теории второго порядка.
В качестве теории первого порядка построим теорию частичного упорядочения. Алфавит: предметные переменные х, у, ..., константы с1, с2,..., единственная предикатная буква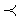 
(будем использовать этот предикат в инфиксной форме, т.е. вместо Р(х,у) будем писать х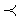у), логические связки &,Ъ,`x.. Из вспомогательных символов выберем только скобки.
Определим формулы. Примем: x, y, z и с - термы t. Если t1 и t2 -термы, то t1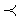t2 -формула Ф. Если Ф1 и Ф2 -формулы, то формулами также будут Ф1&Ф2, Ф1U Ф2, `Ф1.
Аксиоматику составят аксиомы булевой алгебры и две общепредикатные аксиомы, которые мы выразим с помощью связок булевой алгебры
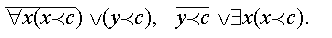
Специальной аксиомой, определяющей транзитивность отношения порядка будет служить предикатная формула
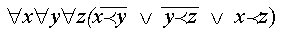
Если отношение порядка должно быть строгим, добавим аксиому
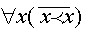
В качестве правила вывода можно использовать modus ponens, приведя его выражение к связкам булевой алгебры:
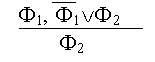
Главное назначение ИП вместе с ИВ состоит в формализации различных теорий с целью проверки их внутренней непротиворечивости, что исторически было необходимо в профессиональной математике. В информатике ИВ и ИП находят применение главным образом для проверки и оптимизации алгоритмов, в частности алгоритмов управления обширными базами данных с использованием отношения порядка и отношения включения (так называемыми реляционными базами данных). Разумеется, материал данного небольшого раздела является лишь ведением в математическую логику, дающим представление о самом предмете и его языке.
