Исчисление высказываний (ИВ). Доказуемость в ИВ.

Исчисле́ние выска́зываний — это формальная теория $\mathcal{L}$ , в которой осуществляется попытка формализации понятий логического закона и логического следования.

Высказывание — это повествовательное предложение, которое истинно или ложно. В классическом исчислении высказываний значимым является лишь истинностное значение высказывания («истина» — 1, «ложь» — 0), поэтому используемые в дальнейшем высказывательные (пропозициональные) переменные могут принимать одно из этих значений.

Логические связки

Кроме высказывательных переменных, в исчислении высказываний используются так называемые логические связки. Если $p\!$ — высказывание, то через $\neg p$ будем обозначать отрицание этого высказывания. Зададим его таблицей истинности:

$p\!$	$\neg p$
$0\!$	$1\!$
$1\!$	$0\!$

Значение двуместных логических связок $\rightarrow$ (импликация), $\vee$ (дизъюнкция) и $\wedge$ (конъюнкция) определются так:

$p\!$	$q\!$	$p\rightarrow q$	$p \wedge q$	$p \vee q$
$0$	$0$	$1$	$0$	$0$
$0$	$1$	$1$	$0$	$1$
$1$	$0$	$0$	$0$	$1$
$1$	$1$	$1$	$1$	$1$

Формулы исчисления высказываний

Атомарные формулы (состоящие из одной высказывательной переменной) являются формулами исчисления высказываний.
Если $p, q\,\!$ — формулы исчисления высказываний, то $(p\rightarrow q)$ , $(p \vee q)$ и $(p \wedge q)$ — формулы исчисления высказываний.
Если $p\!$ — формула исчисления высказываний, то $(\neg p)$ — формула исчисления высказываний.

Тождественно истинные формулы (тавтологии)

Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных. Вот несколько широко известных примеров тождественно истинных формул логики высказываний:

Законы де Моргана:

1) $\neg (p \vee q) \leftrightarrow (\neg p \wedge \neg q)$ ;

2) $\neg (p \wedge q) \leftrightarrow (\neg p \vee \neg q)$ ;

Закон контрапозиции:

$(p\rightarrow q)\leftrightarrow(\neg q\rightarrow \neg p)$ ;

Законы поглощения:

1) $p\vee(p\wedge q)\leftrightarrow p$ ;

2) $p\wedge(p\vee q)\leftrightarrow p$ ;

Законы дистрибутивности:

1) $p\wedge(q\vee r)\leftrightarrow(p\wedge q)\vee(p \wedge r)$ ;

1) $p\vee(q\wedge r)\leftrightarrow(p\vee q)\wedge(p \vee r)$ .

Одним из возможных вариантов (Гильбертовской) аксиоматизации логики высказываний является следующая система аксиом:

$A_1 : A \rightarrow (B \rightarrow A)$ ;

$A_2 : ((A \rightarrow (B \rightarrow C)) \rightarrow ((A \rightarrow B) \rightarrow (A \rightarrow C)))$ ;

$A_3 : A \wedge B \rightarrow A$ ;

$A_4 : A \wedge B \rightarrow B$ ;

$A_5 : A \rightarrow (B \rightarrow (A \wedge B))$ ;

$A_6 : A \rightarrow (A \vee B)$ ;

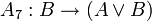$A_7 : B \rightarrow (A \vee B)$ ;

$A_8 : (A \rightarrow C) \rightarrow ((B \rightarrow C) \rightarrow ((A \vee B) \rightarrow C))$ ;

$A_9 : \neg A \rightarrow (A \rightarrow B)$ ;

$A_{10} : (A \rightarrow B) \rightarrow ((A \rightarrow \neg B)\rightarrow \neg A)$ ;

$A_{11} : A\vee\neg A$ .

вместе с единственным правилом:

$\frac{A \rightarrow B, A}{B}$

(Modus ponens)

Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний.

Теорема. Исчисление высказываний непротиворечиво.

Доказательство.

Предположим, что для какой-либо формулы доказуемы секвенции и

Рассмотрим какую-либо интерпретацию исчисления высказываний в множестве

Так как для аксиом утверждение истинно и применение правил вывода не нарушает истинность секвенций, то для всех выводимых (т.е. доказуемых) секвенций утверждение также истинно.

Значит, Поэтому

Но следовательно, что неверно. Таким образом, ИВ непротиворечиво.

5. Теорема о полноте.

6. Теорема о функциональной полноте ИВ.

Рассмотрим теперь главную интерпретацию ИВ. Это будет отображение где — множество всех формул, а — множество всех секвенций. Для атомарных формул значения выберем произвольным образом. На остальные формулы отображение распространим по обычным правилам: где Отображение можно рассматривать как присвоение значений истинности (“истина” или “ложь”) пропозициональным переменным. После того, как такое присвоение произошло, можно говорить об истинности или ложности других формул. Истинность или ложность секвенций определяется следующим образом:

(1) либо при некотором либо

(2)

(3)

(4)

Сформулируем теперь эти определения другими словами. Пусть — формула ИВ, зависящая от пропозициональных переменных (атомарных формул) а — набор из 0 и 1. Будем говорить, что формула истинна на наборе если при . . . , Пусть дана секвенция и — пропозициональные переменные, входящие в какие-либо из формул Секвенция истинна на наборе из 0 и 1, если на этом наборе либо хотя бы одно из ложно, либо истинно. Далее, секвенция истинна на наборе если хотя бы одна из формул на этом наборе ложна. Секвенция истинна на данном наборе, если на этом наборе истинно. Наконец, секвенция считается ложной на любом наборе.

Отметим, что главная интерпретация является частным случаем интерпретации, рассмотренной ранее. Действительно, пусть состоит из одного элемента. Тогда Считаем для ф-лы если и если Непосредственно проверяется, что получится главная интерпретация.

Формула (соответственно, секвенция ) называется тождественно истинной, если она истинна на любом наборе значений истинности пропозициональных переменных. Нетрудно видеть, что тождественная истинность формулы равносильна тождественной истинности секвенции

Лемма 1. Секвенция истинна на наборе в том и только в том случае, если секвенция истинна на этом наборе.

Док-во. Пусть истинна на наборе Тогда выполняется хотя бы одно из условий: 1) хотя бы одна из формул множества ложна на этом наборе; 2) формула ложна на этом наборе; 3) формула истинна на этом наборе. Разберём эти случаи отдельно. 1) Если какая-нибудь формула из ложна, то истинна, а значит, истинна. 2) Если ложна, то истинна, поэтому истинна. 3) Если истинна, то истинна, а значит, также истинна.

Следствие. Секвенция тождественно истинна только в том случае, если секвенция тождественно истинна.

Лемма 2. Секвенция доказуема только в том случае, если секвенция доказуема.

Док-во. Если секвенция имеет доказательство, то по правилу 7 это доказательство можно продолжить и получить Наоборот, если доказана секвенция то из неё по правилу 12 получим Учитывая легко доказываемый факт по правилу 8 получим

Лемма 3. а) Если секвенция доказуема, то она тождественно истинна;

б) если формула доказуема, то она тождественно истинна.

Док-во. Нетрудно проверить, что аксиомы являются тождественно-истинными секвенциями. Также легко проверяется, что применение правил вывода эту тождественную истинность не нарушает. Значит, любая выводимая (доказуемая) секвенция тождественно истинна. Утверждение, касающееся формул, сводится к уже доказанному для секвенций.

Лемма 4. Если формулы и эквивалентны, то булевы функции и совпадают.

Док-во. Можно считать, что формулы и зависят от одних и тех же пропозициональных переменных (переменные, которые не входят в формулу, считаем входящими фиктивно). По условию и — доказуемые секвенции. По лемме 3 они тождественно истинны. Если на каком-либо наборе формула истинна, то так как секвенция истинна, то на этом наборе тоже истинна. Аналогично доказывается, что если истинна на наборе то также истинна на этом наборе. Итак, и истинны на одних и тех же наборах, значит,

Для формулы обозначим через множество наборов на которых она истинна.

Замечание. Лемма 4 на самом деле является следствием более общего результата: если для некоторых формул и секвенция доказуема, то

Теорема 2 (о функциональной полноте ИВ). Пусть в исчислении высказываний бесконечно много атомарных формул. Тогда для любой булевой функции существует формула исчисления высказываний, зависящая от атомарных формул такая, что

Доказательство. Если тождественно равна 0, то в качестве формулы можно взять Если же то, как известно из курса дискретной математики, представима в совершенной дизъюнктивной нормальной форме:

Следовательно, в качестве формулы исчисления высказываний подойдёт формула

Из леммы 3 мы видели, что доказуемыми могут быть только тождественно истинные формулы или секвенции. Оказывается (и это мы докажем в следующей теореме), что верно и обратное: тождественно истинная формула или секвенция имеет формальное доказательство в ИВ. Этот факт мы будем называть полнотой исчисления высказываний.

Теорема 3 (о полноте ИВ).

(а) Формула исчисления высказываний доказуема тогда и только тогда, когда она тождественно истинна.

(б) Секвенция ИВ доказуема тогда и только тогда, когда она тождественно истинна.

Доказательство. Ввиду леммы 2 и следствия из леммы 1 доказуемости (соответственно, тождественные истинности) следующих секвенций эквивалентны: . . . Таким образом можно “перебросить” все формулы, стоящие слева от значка в правую часть и получить секвенцию вида для которой доказуемость (соответственно, тождественная истинность) равносильна доказуемости (соответственно, тождественной истинности) формулы (по определению). Следовательно, нам надо доказать только утверждение (а).

Ввиду леммы 3 нам следует доказать лишь достаточность: если формула тождественно истинна, то она доказуема. Пусть — тождественно истинная формула. По теореме 2 предыдущего раздела существует формула такая, что

Положим . . . , Так как то по лемме 4 тождественно истинна. Но это означает, что формулы тождественно истинны. Рассмотрим какую-нибудь одну из них, например, Если все различны, то не будет тождественно истинной, так как обращается в 0 на таком наборе, где Значит, в какая-либо пропозициональная переменная (скажем, встречается вместе со своим отрицанием. Следовательно, можно преобразовать: Секвенция доказуема по лемме 4 § 1.1. По правилу вывода 4 получим, что секвенция доказуема. Значит, формула доказуема. Аналогично получим, что формулы доказуемы. По правилу 1 получим, что формула доказуема. Следовательно, формула а значит, и формула доказуема.

7. Разрешимость классического исчисления высказываний.

Под разрешимостью мы понимаем существование алгоритма, который по данной формуле (или секвенции определяет, доказуема эта формула (или секвенция) или нет. Такой алгоритм действительно существует.

_____________________________________________________________________

Алфавит ИВ содержит следующие символы:

1) пропозициональные переменные — они обозначают элементарные высказывания — это “кирпичики”, из которых будут формироваться другие, более сложные высказывания;

2) логические связки:

3) служебные символы: “(“, “)”, “,” (левая скобка, правая скобка, запятая);

4) символ

Формула ИВ (высказывание) определяется индуктивно по следующей схеме:

1) атомарные формулы (простейшие) — это пропозициональные переменные;

2) если и — формулы, то — формулы.

Итак, формулами ИВ называются только те слова, записанные в алфавите ИВ, которые получаются по вышеприведённой схеме. Например, если — пропозициональные переменные, то — формулы, а — не формулы.

Пусть дано слово в алфавите Подсловом этого слова мы называем всякое слово вида где началом слова называется подслово вида Слово, в котором нет ни одной буквы, называется пустым словом и обозначается символом Пустое слово является подсловом любого слова. Подформулой формулы мы будем называть подслово слова которое само является формулой.

Доказательство секвенции S в виде дерева – граф, в листьях которого находятся аксиомы, в корне – секвенцию, которую нужно доказать, а все узлы соответствуют переходу 1-12.

Секвенция называется доказуемой, если у нее существует доказательство в виде дерева.

Формула Ф называется доказуемой, если доказуема секвенция |-Ф.

Правило называется допустимым, если его добавление к списку правил вывода не увеличивает множество доказуемых секвенций.