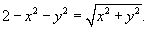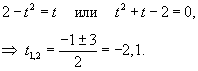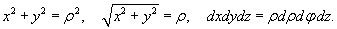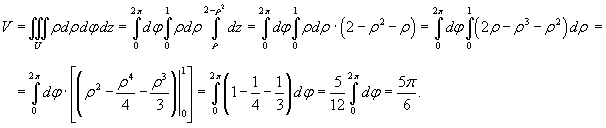|
|
Вычисление массы тела с помощью тройного интеграла.|
Вычисление объемов с помощью тройных интегралов
|
| |
Объем тела U в декартовых координатах Oxyz выражается формулой
В цилиндрических координатах объем тела равен
В сферических координатах, соответственно, используется формула
|
|
Пример 1
|
| |
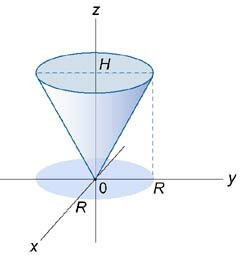
Найти объем конуса высотой H и радиусом основания R (рисунок 2).
Решение.
Конус ограничен поверхностью 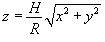 и плоскостью z = H (рисунок 1). В декартовых координатах его объем выражается формулой
Вычислим этот интеграл в цилиндрических координатах, которые изменяются в пределах
Получаем (не забудем включить в интеграл якобиан ρ):
Находим объем конуса:
|
|
Пример 2
|
| |
Найти объем шара x2 + y2 + z2 ≤ R2.
Решение.
Вычислим объем части шара, расположенной в первом октанте ( x ≥ 0, y ≥ 0, z ≥ 0), и затем умножим результат на 8. Получаем
В результате получена известная формула для объема шара радиусом R.
|
|
Пример 3
|
| |
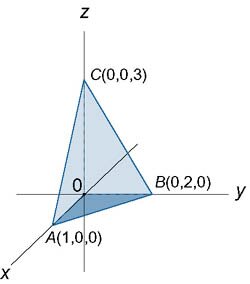
Найти объем тетраэдра, ограниченного плоскостями, проходящими через точки A (1;0;0), B (0;2;0), C (0;0;3), и координатными плоскостями Oxy, Oxz, Oyz (рисунок 2).
Решение.
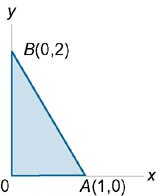
Уравнение прямой AB в плоскости Oxy (рисунок 3) имеет вид: y = 2 − 2 x. При этом переменная x изменяется в интервале 0 ≤ x ≤ 1, а переменная y − в интервале 0 ≤ y ≤ 2 − 2 x.
Составим теперь уравнение плоскости ABC в отрезках. Поскольку плоскость ABC отсекает отрезки 1, 2, 3, соответственно, на осях Ox, Oy и Oz, то ее уравнение имеет вид:
В общем виде уравнение плоскости ABC записывается как
Следовательно, пределы интегрирования по переменной z изменяются в промежутке от z = 0 до 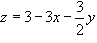 . Теперь можно вычислить объем заданного тетраэдра:
|
|
Пример 4
|
| |
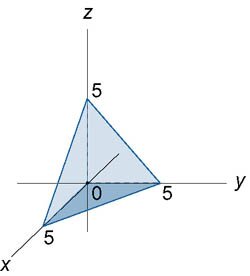
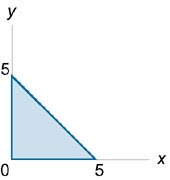
Найти объем тетраэдра, ограниченного плоскостями x + y + z = 5, x = 0, y = 0, z = 0 (рисунок 4).
Решение.
Уравнение плоскости x + y + z = 5 можно переписать в виде
Если положить z = 0, то получим
Следовательно, область интегрирования D в плоскости Oxy ограничена прямой y = 5 − x, как показано на рисунке 5.
Объем тетраэдра будет равен
|
|
Пример 5
|
| |
Найти объем области, ограниченной двумя параболоидами:
Решение.
Исследуем пересечение двух параболоидов (рисунок 6). Поскольку ρ2 = x2 + y2, то уравнения параболоидов записываются в виде
Полагая z1 = z2 для линии пересечения, получаем
Этому значению ρ (рисунок 7) соответствует координата z, равная
Объем данной области выражается с помощью тройного интеграла в виде
В цилиндрических координатах интеграл равен
|
|
Пример 6
|
| |
Вычислить объем эллипсоида
Решение.
Объем эллипсоида удобно вычислить используя обобщенные сферические координаты. Пусть
Поскольку модуль якобиана при трансформации декартовых координат в обобщенные сферические координаты равен
то, следовательно,
Объем эллипсоида выражается через тройной интеграл:
В силу симметрии эллипсоида, мы найдем объем 1/8 его части, расположенной в первом октанте( x ≥ 0, y ≥ 0, z ≥ 0), и затем умножим результат на 8. При этом обобщенные сферические координаты будут изменяться в пределах:
Итак, объем эллипсоида равен
|
|
Пример 7
|
| |
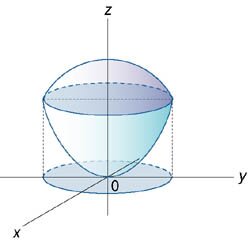
Найти объем тела, ограниченного сферой x2 + y2 + z2 = 6 и параболоидом x2 + y2 = z.
Решение.
Определим сначала линию пересечения поверхностей. Подставляя уравнение параболоида в уравнение сферы, находим:
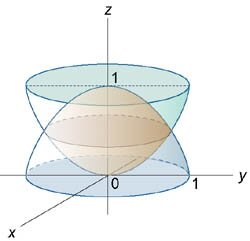
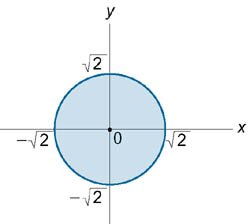
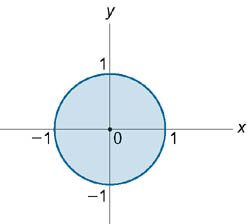
Второй корень z2 = −3 соответствует пересечению сферы с нижней полостью параболоида. Этот случай мы не рассматриваем. Таким образом, перечение тел происходит при z = 2. Очевидно, что проекция области интегрирования на плоскость Oxy имеет вид окружности (рисунок 8), заданной уравнением x2 + y2 = 2.
Сверху область интегрирования ограничена сферической поверхностью, а снизу − параболоидом (рисунок 9). Объем данной области выражается интегралом
Удобно перейти к цилиндрическим координатам:
где ρ2 = x2 + x2 и интеграл включает якобиан ρ. Получаем:
Заменим ρ2 = t. Здесь t = 0 при ρ = 0, и, соответственно, t = 2 при ρ = √2.
Окончательно вычисляем объем тела:
|
|
Пример 8
|
| |
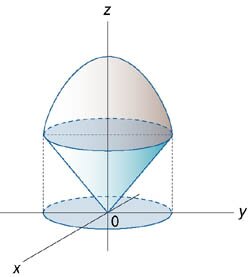
Вычислить объем тела, ограниченного параболоидом z = 2 − x2 − y2 и конической поверхностью 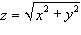 .
Решение.
Исследуем сначала пересечение двух заданных поверхностей. Приравнивая координаты z, получаем уравнение
Пусть x2 + y2 = t2. Тогда
В контексте данной задачи смысл имеет лишь корень t = 1, то есть
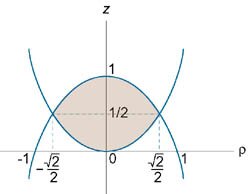
Итак, обе поверхности пересекаются при z = 1, и сечение представляет собой круг (рисунок 10)
Область интегрирования сверху ограничена параболоидом , а снизу − конусом (рисунок 11). Для вычисления объема области перейдем к цилиндрическим координатам:
В результате находим
|
|

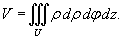
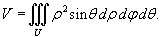
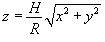 и плоскостью z = H (рисунок 1). В декартовых координатах его объем выражается формулой
и плоскостью z = H (рисунок 1). В декартовых координатах его объем выражается формулой
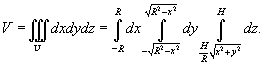
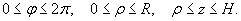
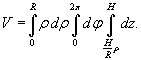
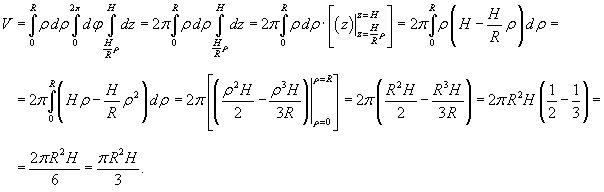
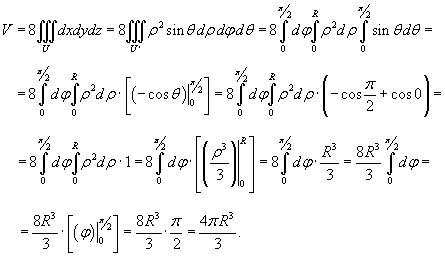
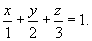
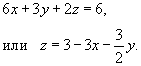
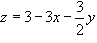 . Теперь можно вычислить объем заданного тетраэдра:
. Теперь можно вычислить объем заданного тетраэдра:
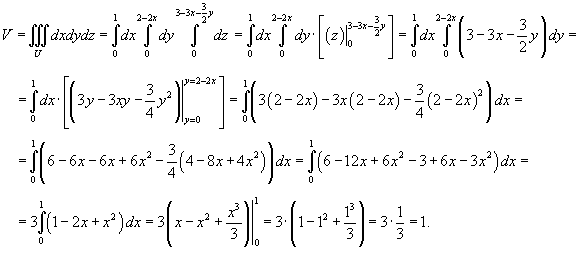
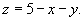
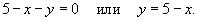
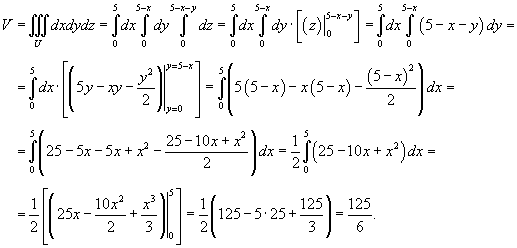
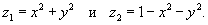
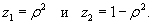
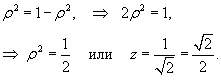
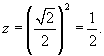
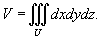
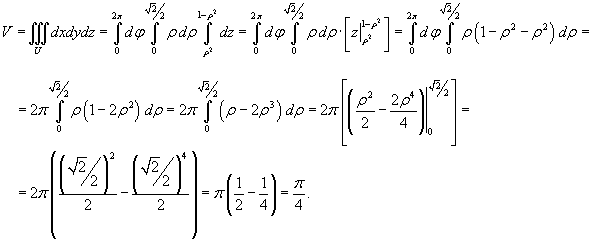
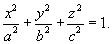
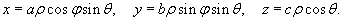
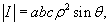
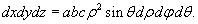
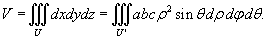
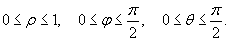
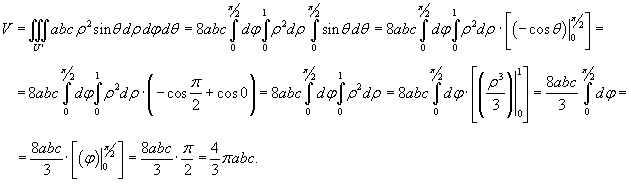
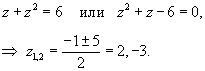
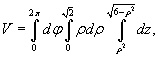
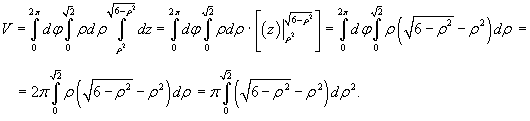
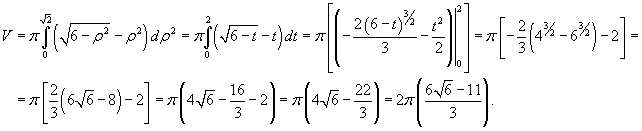
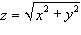 .
.