Тройной интеграл.

Тройным интегралом называют кратный интеграл с $d = 3$ .

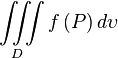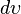$iiintlimits_{D}{fleft( P right)dupsilon }$ Здесь $dupsilon$ — элемент объема в рассматриваемых координатах.

В прямоугольных координатах $iiint f(x,y,z) , dx , dy , dz$ , где $dxdydz$ является элементом объема в прямоугольных координатах.

Выражение тройного интеграла через цилиндрические координаты [править]

Объем в цилиндрических координатах

Аналогично в некоторых случаях тройной интеграл проще считать не в прямоугольных, а в цилиндрических координатах. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

$left{ begin{align} & x=rcos varphi \ & y=rsin varphi \ & z=h \ end{align} right.$

Модуль якобиана отображения равен $r$ . Таким образом получаем, что

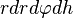$iiintlimits_{D}{fleft( x,y,z right)dxdydz}=iiintlimits_{{{D}'}}{fleft( r,varphi ,h right)rdrdvarphi dh}$

Здесь $rdrdvarphi dh$ является элементом объема в цилиндрических координатах.

Выражение тройного интеграла через сферические координаты [править]

Объем в сферических координатах

Кроме цилиндрических можно также переходить и в сферические координаты. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

$left{ begin{align} & x=rsin theta cos varphi \ & y=rsin theta sin varphi \ & z=rcos theta \ end{align} right.$

Модуль якобиана отображения равен ${{r}^{2}}sin theta$ . Таким образом получаем, что

$iiintlimits_{D}{fleft( x,y,z right)dxdydz}=iiintlimits_{{{D}'}}{fleft( r,varphi ,theta right){{r}^{2}}sin theta drdvarphi dtheta }$

Здесь ${{r}^{2}}sin theta drdvarphi dtheta$ является элементом объема в сферических координатах.

ПРИМЕРЫ

Задача1 Вычислить тройной интеграл , где область ограничена поверхностями, , , .

Решение
Поверхности, ограничивающие область интегрирования, являются плоскостями, а область primer_matanaliz34_clip_image004_0001.gi является тетраэдром, который определяется системой неравенств
Изобразим область .

Проекцией области на плоскость является прямоугольный треугольник,

определяемый системой неравенств

Задача2 С помощью тройного интеграла вычислить объём тела, ограниченного координатными плоскостями и плоскостью . Изобразить данное тело и его проекцию на плоскость.

Решение
Если , то где V-объём области интегрирования.
Изобразим данное тело и его проекцию на плоскости primer_matanaliz35_clip_image004_0000.gi .