Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
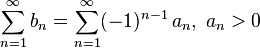
Признак Лейбница
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
|
Пусть для знакочередующегося ряда
выполняются следующие условия:
Тогда этот ряд сходится. |
Если, выполнены все условия, и ряд из модулей (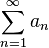 ) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность
) сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность  существенна.
существенна.
Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
Пример
 . Ряд из модулей имеет вид
. Ряд из модулей имеет вид  — это гармонический ряд, который расходится.
— это гармонический ряд, который расходится.
Теперь воспользуемся признаком Лейбница:
- знакочередование выполнено

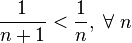
 .
.
Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.
Оценка остатка ряда Лейбница [править]
Из доказательства признака Лейбница следует, что сумма знакопеременного сходящегося ряда меньше по модулю первого члена ряда. Поскольку любой остаток ряда rn является также рядом Лейбница, то для него справедливо:
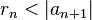 .
.


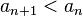 (монотонное убывание {an})
(монотонное убывание {an})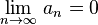 .
.