Интегральный признак Коши-Маклорена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на  , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде.
Формулировка теоремы
|
Пусть для функции f(x) выполняется:
Тогда ряд |
О: Знакопеременным числовым рядом называется ряд
который содержит как положительные, так и отрицательные члены.
Знакочередующийся ч.р. является частным случаем знакопеременного ч.р.
Т. (признак абсолютной сходимости): Если для знакопеременного ч.р. сходится ряд
сходится ряд составленный из абсолютных величин его членов, то ряд
составленный из абсолютных величин его членов, то ряд сходится
сходится
Обозначим — сумма положительных
— сумма положительных
членов в — сумма абсолютных величин отрицательных чле-
— сумма абсолютных величин отрицательных чле-
нов в
Тогда

Последовательности частичных сумм возрастают и ограничены, так как
возрастают и ограничены, так как поэтому
поэтому
 и
и
Данный ряд по определению сходится


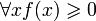 (функция принимает неотрицательные значения)
(функция принимает неотрицательные значения) (функция монотонно убывает)
(функция монотонно убывает)
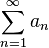 и несобственный интеграл
и несобственный интеграл 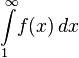 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.