Радикальный признак Коши — признак сходимости числового ряда:
|
Если для числового ряда
с неотрицательными членами существует такое число |
Предельная форма [править]
Условие радикального признака равносильно следующему:
![lim_{ntoinfty}sqrt[n]{a_n}<1](http://upload.wikimedia.org/math/9/1/a/91a579e5d480620139a0121cca6450ba.png)
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
|
Если для ряда
если если если |
Доказательство
1. Пусть  . Очевидно, что существует такое
. Очевидно, что существует такое  , что
, что  . Поскольку существует предел
. Поскольку существует предел ![lim_{n to infty}sqrt[n]{a_n}=l](http://upload.wikimedia.org/math/4/d/2/4d2ae3e89ea5fad0263abe94156bf496.png) , то подставив в определение предела выбранное
, то подставив в определение предела выбранное  получим:
получим:
![vert sqrt[n]{a_n} - l vert < varepsilon](http://upload.wikimedia.org/math/d/5/5/d551092de67775c998c80194ce0f5e56.png)
Раскрыв модуль, получаем:
![- varepsilon < sqrt[n]{a_n} - l < varepsilon](http://upload.wikimedia.org/math/1/c/2/1c2c65097e826f614647f5a082868fb1.png)
![l - varepsilon < sqrt[n]{a_n} < l + varepsilon](http://upload.wikimedia.org/math/5/b/c/5bc4f6893f01f22957b48b42736f9b8d.png)
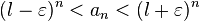
Поскольку  , то ряд
, то ряд  сходится. Следовательно, по признаку сравнения ряд
сходится. Следовательно, по признаку сравнения ряд 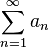 тоже сходится.
тоже сходится.
2. Пусть  . Очевидно, что существует такое
. Очевидно, что существует такое  , что
, что  . Поскольку существует предел
. Поскольку существует предел ![lim_{n to infty}sqrt[n]{a_n}=l](http://upload.wikimedia.org/math/4/d/2/4d2ae3e89ea5fad0263abe94156bf496.png) , то подставив в определение предела выбранное
, то подставив в определение предела выбранное  получим:
получим:
![vert sqrt[n]{a_n} - l vert < varepsilon](http://upload.wikimedia.org/math/d/5/5/d551092de67775c998c80194ce0f5e56.png)
Раскрыв модуль, получаем:
![- varepsilon < sqrt[n]{a_n} - l < varepsilon](http://upload.wikimedia.org/math/1/c/2/1c2c65097e826f614647f5a082868fb1.png)
![l - varepsilon < sqrt[n]{a_n} < l + varepsilon](http://upload.wikimedia.org/math/5/b/c/5bc4f6893f01f22957b48b42736f9b8d.png)
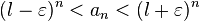
Поскольку  , то ряд
, то ряд  расходится. Следовательно, по признаку сравнения ряд
расходится. Следовательно, по признаку сравнения ряд 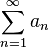 тоже расходится.
тоже расходится.
Примеры
1. Ряд

сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
![lim_{n to infty}sqrt[n]{a_n}=frac{1}{2}](http://upload.wikimedia.org/math/e/b/f/ebf1d114bf26d5d750ecb4c30eb504c8.png)
2. Рассмотрим ряд

![lim_{n to infty}sqrt[n]{a_n} = lim_{n to infty} {left(frac{n-1}{n+1}right)}^{n-1} = lim_{n to infty} {left(1 - frac{2}{n+1}right)}^{n-1} = e^{-2} < 1 Rightarrow](http://upload.wikimedia.org/math/f/0/2/f02b1b17b2c2453fa8c1882e1c432146.png) ряд сходится.
ряд сходится.


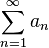
 ,
,  , что, начиная с некоторого номера, выполняется неравенство
, что, начиная с некоторого номера, выполняется неравенство ![sqrt[n]{a_n}<d](http://upload.wikimedia.org/math/2/3/a/23a4d3b1f41b233f1b1a0a56a8771ce2.png) , то данный ряд сходится.
, то данный ряд сходится.![sum_{n=1}^infty a_n (a_n ge ; 0) existslim_{n to infty}sqrt[n]{a_n}=l ;](http://upload.wikimedia.org/math/5/e/9/5e9a079703c906d55e5bc2ae4eb82a8c.png) , то
, то ряд сходится,
ряд сходится, вопрос о сходимости ряда остается открытым.
вопрос о сходимости ряда остается открытым.