Длина дуги кривой.

Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).

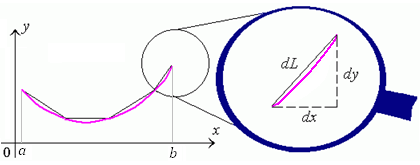
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.

Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:

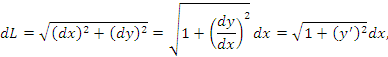(1)

где y ' – производная функции y = f(x) по переменной x.

Длина дуги равна сумме длин составляющих ее элементов:

_____________________________________________________________________________________________________________

______________________________________________________________________________________________________________

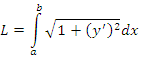Из Википедии:

Евклидово пространство

Для евклидова пространства длина отрезка кривой определяется как точная верхняя грань длин вписанных в кривую ломаных. Для наглядности рассмотрим трёхмерное пространство. Пусть непрерывная кривая $gamma$ задана параметрически:

$x=x(t),quad y=y(t),quad z=z(t)qquadqquad$ ,

(1)

Приближение кривой ломаными

где $~a leqslant t leqslant b$ . Рассмотрим всевозможные разбиения интервала значений параметра $[a,b]$ на $m$ отрезков: $~a=x_0<x_1<dots<x_m=b$ . Соединив точки кривой $~gamma(x_0), dots, gamma(x_m)$ отрезками прямых, мы получим ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных.

Всякая непрерывная кривая имеет длину, конечную или бесконечную. Если все функции в (1) являютсяфункциями ограниченной вариации, то длина кривой существует и конечна. В математическом анализе выводится формула для вычисления длины $s$ отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:

$s=intlimits_a^b sqrt{{x'}^2(t) + {y'}^2(t) + {z'}^2(t)}, dt$

(2)

Формула подразумевает, что 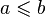$a leqslant b$ и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.

В n-мерном случае вместо (2) имеем аналогичную формулу:

$s=intlimits_a^b sqrt{sumlimits_{k=1}^n {f'_k}^2 (t)} , dt$ .

Можно также вычислить длину кривой $gamma$ через криволинейный интеграл I рода:

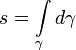
$s= intlimits_gamma dgamma$

Длина дуги как параметр

Кривая допускает бесчисленное множество различных способов параметрического задания уравнениями вида (1). Среди них особое значение имеет так называемая естественная параметризация, когда параметром служит длина дуги кривой, отсчитываемая от некоторой фиксированной точки.

Среди преимуществ такой параметризации:

Производная радиус-вектора $frac{dmathbf{r}} {dt}$ имеет единичную длину и поэтому совпадает с единичным вектором касательной.
$frac{d^2mathbf{r}} {dt^2}$ по длине совпадает с кривизной кривой, а по направлению — с её главной нормалью.

Евклидова плоскость

Если плоская кривая задана уравнением $y=f(x),$ то её длина равна:

$s=intlimits_a^b sqrt{1 + {f'}^2(x)}, dx.$

В полярных координатах $(r, varphi):$

$s=intlimits_a^b sqrt{r^2+left(frac{dr}{dvarphi}right)^2} , dvarphi.$

Риманово пространство

В n-мерном римановом пространстве с координатами $x^1 cdots x^n$ кривая задаётся параметрическими уравнениями:

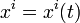$x^i=x^i(t) qquadqquad$ ,

((3))

Длина кривой в римановом пространстве задаётся формулой:

$s = intlimits_a^b sqrt{ g_{ij}{dx^iover dt}{dx^jover dt}},dt$ ,

где : $g_{ij}$ — метрический тензор. Пример: кривая на поверхности в $mathbb{R}^3$ .

Общее метрическое пространство

В более общем случае произвольного метрического пространства $(X,rho)$ длиной $S$ кривой называется вариация задающего кривую отображения, то есть длина кривой $gamma:[a,b]to X$ определяется согласно формуле:

$s=sup sumlimits_{k=0}^m rho(gamma(x_{k+1}),gamma(x_k)),$

где верхняя грань берётся, как и ранее, по всем разбиениям 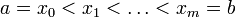$a=x_0<x_1<dots<x_m=b$ отрезка $[a,b]$ .