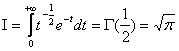Признак сравнения несобственных интегралов.

Для исследования сходимости и расходимости несобственных интегралов применяется признак сравнения:

Пусть функция f(x) и g(x) удовлетворяют неравенству: 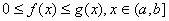и несобственный интеграл  сходится. Тогда сходится и несобственный интеграл .

Доказательство: В силу сходимости  по критерию Коши для функции 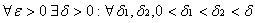, выполняется неравенство 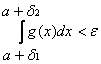. Но тогда, ввиду неравенств:  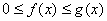аналогично неравенство будет справедливо и для функции f(x), т.е.

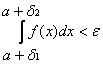
Следовательно, по критерию Коши существует предел:

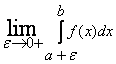, т.е. этот интеграл сходится.

Замечание1: Аналогичный признак сравнения справедлив и для несобственных интегралов 2 рода.

Замечание2: Отрицанием признака сравнения будет следующее утверждение: если несобственный интеграл  расходится, то расходится и несобственный интеграл .

Эйлеровы интегралы G(a) и B(a, b).

Определим функцию G(a) равенством:

.

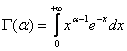Покажем, что интеграл сходится при a > 0. Представим этот интеграл в виде суммы двух интегралов:

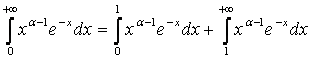
и докажем сходимость каждого из этих интегралов при a > 0.

Обозначим 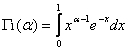 и .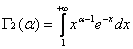

Если xÎ(0, 1], то: 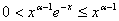. Так как интеграл 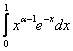, как это было доказано выше сходится при 1 - a< 1, т.е. при a>0, то по признаку сравнения интеграл  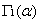сходится при a>0. Если xÎ[1, + 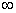) , то для некоторой константы c>0 выполняется неравенство: .

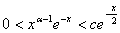 Заметим, что 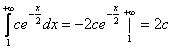, т.е. этот интеграл сходится при любых aÎR. Следовательно, функция Эйлера G(a) = G₁(a) + G₂(a) определена для всехa>0.

Далее, определим функцию B(a, b) = 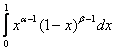 и докажем, что эта функция определена для любых a>0 и b>0.

Обозначим: 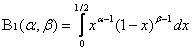 и .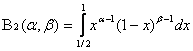

Если xÎ(0, 1/2], то 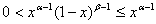. Интеграл  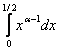сходится по признаку сравнения 1 - a<1, т.е. при a>0 и при любых значениях b. Заметим, что, если в интеграле B₂(a, b) сделать замену t = 1 – x, то мы B₁(b, a), который, как мы выяснили, сходится при b>0 и при любых a.

Следовательно, функция Эйлера B(a, b) = B₁(a, b) + B₂(a, b) определена для любых a>0 и b>0. Отметим (без доказательства) следующие свойства интегралов Эйлера:

1)      G(1) = 1

2)      G(a + 1) = aG(a),  a>0

3)      G(n + 1) = n!, nÎN

4)      G(a)G(1 - a) =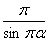 , 0<a<1

5)      G(1/2) =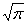 

6)      B(a, b) =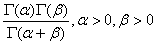 

Пример:

Вычислить интеграл вероятности .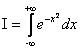

В силу чётности функции 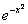 интеграл вероятности можно представить в виде:

 .

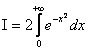Сделав в этом интеграле замену t = x² , получим следующий интеграл: