Волновое уравнение

Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением

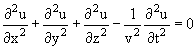(1)

где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены v → -v.

В многомерном случае однородное волновое уравнение записывается в виде

$Delta u=frac{1}{v^2}frac{partial^2 u}{partial t^2}$ ,

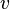где $~Delta$ — оператор Лапласа, $~u=u(x,t)$ — неизвестная функция, $~tin mathbb R$ — время, $~xin mathbb R^n$ — пространственная переменная, $~v$ — фазовая скорость.

В одномерном случае уравнение называется также уравнением колебания струны или уравнением продольных колебаний стержня и записывается в виде

$frac{partial^2 u}{partial x^2}=frac{1}{v^2}frac{partial^2 u}{partial t^2}$ .

Оператор Д’Аламбера

Разность 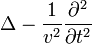$Delta - frac{1}{v^2} frac{partial^2}{partial t^2}$ называется оператором Д’Аламбера и обозначается как $square$ (разные источники используют разный знак). Таким образом, с использованием оператора Д'Аламбера (даламбертиана) однородное волновое уравнение записывается как:

$square u = 0$

Неоднородное уравнение

Допустимо также рассматривать неоднородное волновое уравнение

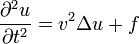$frac{partial^2 u}{partial t^2}=v^2Delta u + f$ ,

где $f = f(x,t)$ — некая заданная функция внешнего воздействия (внешней силы).

Стационарным вариантом волнового уравнения является уравнение Лапласа (уравнение Пуассона в неоднородном случае).

Задача нахождения нормальных колебаний системы, описываемой волновым уравнением, приводит к задаче на собственные значения дляуравнения Лапласа, то есть к нахождению решений уравнения Гельмгольца, получающегося подстановкой

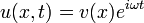$u(x,t) = v(x) e^{iomega t}$ или $u(x,t) = v(x), mathop{rm cos},(omega t)$ .

РЕШЕНИЕ

Существует аналитическое решение гиперболического уравнения в частных производных. В евклидовом пространстве произвольной размерности оно называется формулой Кирхгофа. Частные случаи: для колебания струны ( $mathbb{R}^1$ ) — формула Д’Аламбера, для колебания мембраны ( $mathbb{R}^2$ ) —формула Пуассона.

Формула Д'Аламбера

Решение одномерного волнового уравнения (здесь $v = a$ — фазовая скорость)

$u_{tt}=a^2 u_{xx} + f(x,t)quad$ (функция $f(x,t)$ соответствует вынуждающей внешней силе)

с начальными условиями

$u(x,0)=varphi(x),quad u_t(x,0)=psi(x)$

имеет вид

$u(x,t)=frac{varphi(x+at)+varphi(x-at)}{2}+frac{1}{2a}intlimits^{x+at}_{x-at}{psi(alpha)d alpha}+frac{1}{2a}intlimits^t_0intlimits^{x+a(t-tau)}_{x-a(t-tau)} f(s, tau)ds dtau$

Интересно заметить, что решение однородной задачи

$u_{tt}=a^2 u_{xx}$ ,

имеющее следующий вид

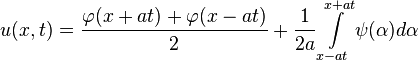
$u(x,t)=frac{varphi(x+at)+varphi(x-at)}{2}+frac{1}{2a}intlimits^{x+at}_{x-at}{psi(alpha)d alpha}$

может быть представлено в виде

$u(x,t)= f_1(x+at) + f_2(x-at)$

где

$f_1(x)= frac{varphi(x)}{2} + frac{1}{2a}intlimits^{x}_{0}{psi(alpha)d alpha}$

$f_2(x)= frac{varphi(x)}{2} + frac{1}{2a}intlimits^{0}_{x}{psi(alpha)d alpha}$

В таком случае говорят, что решение представлено в виде суммы бегущих волн, а функции 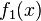$f_1(x)$ и $f_2(x)$ - это профили волн, бегущих, соответственно, влево и вправо. В рассматриваемом случае профили волн со временем не изменяются.

В многомерном случае также решение задачи Коши может быть разложено в бегущие волны, однако уже не в сумму, а в интеграл, поскольку направлений становится бесконечно много. Это делается элементарно при помощи преобразования Фурье