1.Метод эквивалентного генератора в расчётах цепей постоянного тока. 2. Параметры периодических несинусоидальных величин.

1.

 

 При решении задач по электротехнике, зачастую требуется знать режим работы не всей цепи, а только одной определённой ветви. Для определения параметров такой ветви существуетметод эквивалентного генератора.

  Суть метода эквивалентного генератора состоит в нахождении тока в одной выделенной ветви, при этом остальная часть сложной электрической цепи заменяется эквивалентным ЭДС Е_экв, с её внутренним сопротивлением r_экв. Эту часть цепи, в которую входит источник ЭДС, называют эквивалентным генератором или активным двухполюсником, откуда и название метода.

  Для наглядности рассмотрим схему представленную ниже. Допустим, что R₁=5 Ом, R₂=7 Ом, R₃=10 Ом, R_ab=3 Ом, E=10 В.

 

  Согласно методу эквивалентного генератора получим схему

 

  Искомый ток I_ab находится по закону Ома для полной цепи

 

  Для нахождения тока нужно узнать Е_экв и r_экв с помощью режимов эквивалентного генератора.

    Нахождение эквивалентного ЭДС

  Для того чтобы найти эквивалентную ЭДС, нужно рассмотреть режим холостого ходагенератора, другими словами нужно отсоединить исследуемую ветвь ab, тем самым избавив генератор от нагрузки, после чего он будет работать на так называемом холостом ходу.

                  

 

  Напряжение холостого хода U_х, будет равно эквивалентной ЭДС E_экв. Таким образом мы можем найти E_экв.

 

    Нахождение эквивалетного сопротивления

  Следующим этапом решения задачи будет нахождение эквивалентного сопротивления r_экв. Можно воспользоваться режимом короткого замыкания генератора, при котором сопротивление R_ab отсутствует, но в более сложных схемах это может привести к более громоздким расчётам, поэтому найдем r_экв как входное сопротивление пассивного двухполюсника. Пассивным называется двухполюсник у которого отсутствуют источники ЭДС. Простыми словами нужно убрать во внешней цепи источник ЭДС и найти сопротивление цепи, так и поступим.

    

  Эквивалентное сопротивление r_экв равно ( тем, кто не умеет находить эквивалентное сопротивление, нужно прочитать статью виды соединения проводников )

 

 

   Нахождение тока

  Итак, найдя эквивалентные ЭДС и сопротивление, мы можем найти силу тока в ветви ab

 

  На этом всё, ток в нужной ветви найден, а значит, задача решена методом эквивалентного генератора.

 

2.

Предыдущие лекции были посвящены анализу электрических цепей при синусоидальных токах и напряжениях. На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников.

На практике к несинусоидальности напряжений и токов следует подходить двояко:

• в силовой электроэнергетике несинусоидальные токи обусловливают в общем случае дополнительные потери мощности, пульсации момента на валу двигателей, вызывают помехи в линиях связи; поэтому здесь необходимо «всеми силами» поддержание синусоидальных режимов;
• в цепях автоматики и связи, где несинусоидальные токи и напряжения лежат в основе принципа действия электротехнических устройств, задача наоборот заключается в их усилении и передаче с наименьшими искажениями.

В общем случае характер изменения величин может быть периодическим, почти периодическим и непериодическим. В данном разделе будут рассматриваться цепи только с периодическими переменными.

Периодическими несинусоидальными величинами называются переменные, изменяющиеся во времени по периодическому несинусоидальному закону. Причины возникновения несинусоидальных напряжений и токов могут быть обусловлены или несинусоидальностью источника питания или (и) наличием в цепи хотя бы одного нелинейного элемента. Кроме того, в основе появления несинусоидальных токов могут лежать элементы с периодически изменяющимися параметрами.

В качестве примера на рис. 1,а представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (см. рис. 1,б).

 

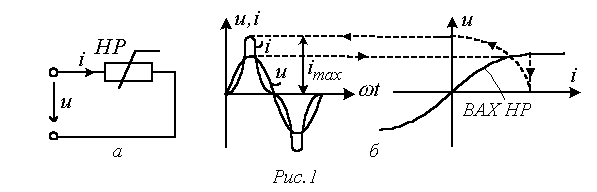
Характеристики несинусоидальных величин

Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):

1. Максимальное значение -  .
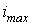2. Действующее значение -  .
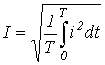3. Среднее по модулю значение -  .
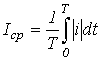4. Среднее за период значение (постоянная составляющая) -  .
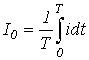5. Коэффициент амплитуды (отношение максимального значения к действующему) -  .
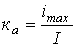6. Коэффициент формы (отношение действующего значения к среднему по модулю) -  .
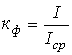7. Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) -  .
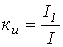8. Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) -  .

 

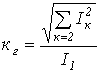Разложение периодических несинусоидальных 
кривых в ряд Фурье

Из математики известно, что всякая периодическая функция 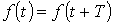 , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.

При разложении в ряд Фурье функция представляется следующим образом:

 

.

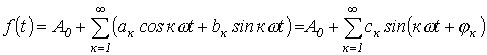(1)

 

Здесь 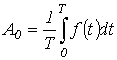 - постоянная составляющая или нулевая гармоника;  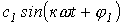 - первая (основная) гармоника, изменяющаяся с угловой частотой  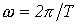, где Т – период несинусоидальной периодической функции.

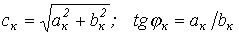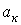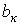В выражении (1)  , где коэффициенты   и   определяются по формулам

 ;

 .

 

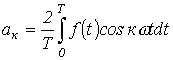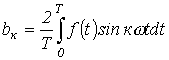Свойства периодических кривых, обладающих симметрией

Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих симметрией, задача существенно упрощается, поскольку из их разложения выпадают целые спектры гармоник. Знание свойств таких кривых позволяет существенно сэкономить время и ресурсы при вычислениях.

К данному типу относятся кривые, удовлетворяющие равенству 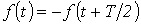  (см. пример на рис. 2). В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е.  .

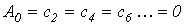К данному типу относятся кривые, для которых выполняется равенство 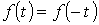 (см. пример на рис. 3). В их разложении отсутствуют синусные составляющие, т.е.  .

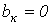К этому типу относятся кривые, удовлетворяющие равенству 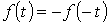  (см. пример на рис. 4). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е.  .

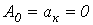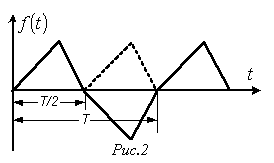1. Кривые, симметричные относительно оси абсцисс.
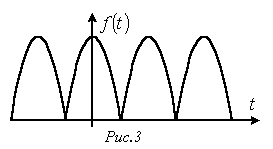2. Кривые, симметричные относительно оси ординат.
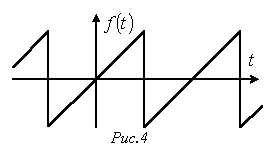3. Кривые, симметричные относительно начала координат.

Действующее значение периодической несинусоидальной переменной

Как было показано выше, действующим называется среднеквадратичное за период значение величины:

 .

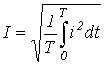При наличии аналитического выражения функции i(t) и возможности взятия интеграла от ее квадрата действующее значение i(t) определяется точно. Однако в общем случае на практике действующее значение переменной определяется на основе информации о  действующих значениях конечного ряда гармонических.

Пусть 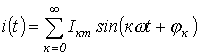 . Тогда

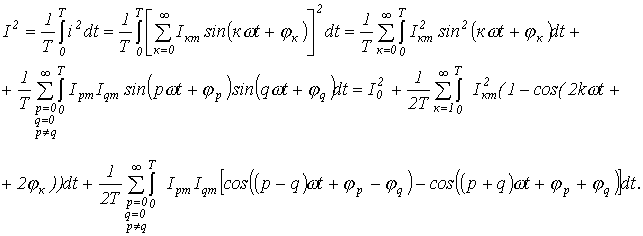
Очевидно, что каждый из интегралов от тригонометрических функций в последнем выражении равен нулю. Таким образом,

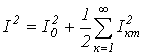
или

 .

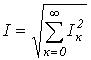Аналогичные выражения имеют место для ЭДС, напряжения и т.д.

 

Мощность в цепях периодического несинусоидального тока

Пусть 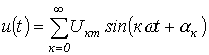  и  .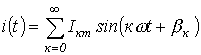

Тогда для активной мощности можно записать

 .

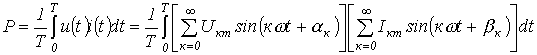Как было показано при выводе соотношения для действующего значения несинусоидальной переменной, среднее за период значение произведения синусоидальных функций различной частоты равно нулю. Следовательно,

 ,

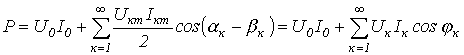где  .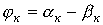

Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармонических:

 .

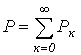Аналогично для реактивной мощности можно записать

 .

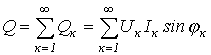Полная мощность

 ,

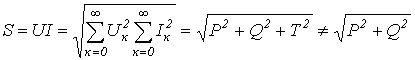где Т – мощность искажений, определяемая произведениями действующих значений разнопорядковых гармонических тока и напряжения.