Биномиальное распределение — дискретное распределение вероятностей случайной величины принимающей целочисленные значения
с вероятностями:
Данное распределение характеризуется двумя параметрами: целым числом называемым числом испытаний, и вещественным числом
называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из
независимых испытаний, в каждом из которых может произойти "успех" с вероятностью
то случайная величина, равная числу успехов во всей серии, имеет указанное распределение.
Дискретная случайная величина имеет распределение Пуассона с параметром λ, если:

Распределение Пуассона также называется распределением редких событий.
Распределение Пуассона - это дискретное распределение, являющееся одним из важных предельных случаев биномиального распределения.
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Числовые характеристики
Числовые характеристики случайных величинМатематическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений хi с вероятностями рi , называется сумма:
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
|
Свойства математического ожидания:
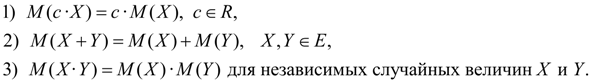
Дисперсия. Дисперсией случайной величины Х называется число:
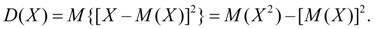 (8)
(8)
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М ( Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
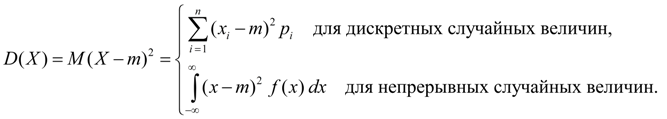
Здесь m = М ( Х ).
Свойства дисперсии:
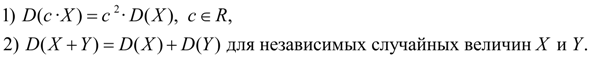
Среднее квадратичное отклонение:
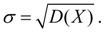 (11)
(11)
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.


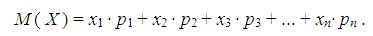 (6а)
(6а)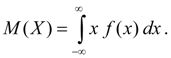 (6б)
(6б)