Обыкновенное дифференциальное уравнение 1-го порядка

Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнения входят явно производные искомых функций до некоторого порядка. Если неизвестными являются функции двух или более переменных, то уравнения называются уравнениями в частных производных. В противном случае, то есть если искомая функция зависит только от одного вещественного независимого переменного, уравнения называются обыкновенными дифференциальными уравнениями. В этом курсе будем иметь дело только с последними.

Так как во многих физических приложениях независимым переменным, от которого зависят неизвестные искомые функции, является время, то в дальнейшем, как правило, независимое переменное будет обозначаться через t. Неизвестные функции будут обозначаться через x, y, z и т.д.

Рассмотрим в первую очередь одно дифференциальное уравнение первого порядка. Общий вид такого уравнения следующий:

Здесь t - независимое переменное, x - неизвестная функция, зависящая от t.  - ee производная. F - заданная функция трех вещественных переменных. Функция F, вообще говоря, может быть задана не для всех значений своих аргументов, поэтому следует говорить об области W задания функции F, имея в виду область координатного пространства трех (вещественных) переменных t, x, .

Уравнение (1.1) называется уравнением первого порядка потому, что в него входит лишь производная первого порядка от неизвестной функции x.

Решением уравнения (1.1) называется такая функция x = j(t) независимого переменного t, определения на некотором интервале r1  <  t  <  r2 (случаи r1 = -Ґ и r2 = + Ґ не исключаются), которая дифференцируема в каждой точке этого интервала и при подстановке ее вместо x в соотношение (1.1) мы получаем тождество (по t) на всем интервале r1 < t < r2.

Интервал r1 < t < r2 называется интервалом определения решения j(t).

Очевидно, что подстановка функции x = j(t) в соотношение (1.1) возможна только в том случае, когда точка с координатами (t, j(t), ) принадлежит области W определения функции F при произвольном t из интервала r1 < t < r2.

Соотношение (1.1) связывает три переменные: t, x, . В некоторых случаях из (1.1) переменная  может быть выражена в виде однозначной функции переменных t, x. В этом случае дифференциальное уравнение (1.1) равносильно дифференциальному уравнению вида

МОНОТОННОСТЬ

Исследование функций должно начинаться с установления области определения и интервалов монотонности. Для этого студент должен обладать хорошими знаниями поведения элементарных функций и последующим теоретическим материалом.

Функция 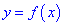 называется возрастающей на интервале  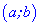если для любых двух точек  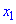и 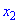 с этого промежутка и таких, что  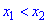выполняется неравенство

 .

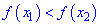Для того чтобы функция 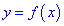 была убывающей на интервале  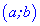необходимо, чтобы для любых  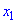и 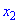 , принадлежащих к этому интервалу и удовлетворяющих условию  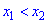исполнялось неравенство
 .

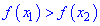Как возрастающие, так и убывающие функции называются монотонными, а интервалы в которых

функция возрастает или убывает – интервалами монотонности.

Область возрастания и убывания функции 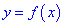 характеризуется знаком ее производной: если в

некотором интервале производная больше нуля 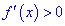 , то функция возрастает в этом интервале;

если же наоборот 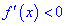 – то функция убывает в этом интервале.

Выпуклость, вогнутость функции, точка перегиба.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Посмотрите на чертеж, иллюстрирующий эти определения.

Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.

На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

Стационарные точки – это значения аргумента, при которых производнаяфункции обращается в ноль.

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигаетсяэкстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.