Теорема Коши́ о среднем значении.
|
Пусть даны две функции
тогда существует
(Если убрать условие 4, то необходимо, например, усилить условие 3: g'(x) не должна обращаться в нуль нигде в интервале |
Геометрически это можно переформулировать так: если  и
и  задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр
задают закон движения на плоскости (то есть определяют абсциссу и ординату через параметр  ), то на любом отрезке такой кривой, заданном параметрами
), то на любом отрезке такой кривой, заданном параметрами  и
и  , найдётся касательный вектор, коллинеарный вектору перемещения от
, найдётся касательный вектор, коллинеарный вектору перемещения от 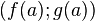 до
до  .
.
[править] Доказательство
Для доказательства введём функцию
 |
Для неё выполнены условия теоремы Ролля: на концах отрезка её значения равны 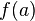 . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции  равна нулю, а
равна нулю, а 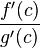 равна как раз необходимому числу.
равна как раз необходимому числу.


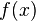 и
и  такие, что:
такие, что:![[a,b]](http://upload.wikimedia.org/math/5/f/c/5fc1fbc48b5a353c0095a0f55f520e32.png) ;
; и
и  конечны на интервале
конечны на интервале 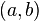 ;
; ;
; , для которой верно:
, для которой верно: .
. .)
.)