Пусть функции φ1,…,φn определены в некоторой окрестности точки x0∈Rm и непрерывны в точке x0, а функция f(y)=f(y1,…,yn)определена в окрестности точки y0=(φ1(x0),…,φn(x0)) и непрерывна в точке y0. Тогда в некоторой окрестности точки x0 определена сложная функция. Φ(x)=f(φ1(x),…,φn(x))причем функция Φ(x) непрерывна в точке x0.
Воспользуемся доказательством в случае одной переменной.
Теорема о непрерывности сложной функций
Пусть функция φ(t) непрерывна в точке t0 и функция f(x) непрерывна в точке x0=φ(t0). Тогда функция f(φ(t)) непрерывна в точке t0.
Доказательство:
Для доказательства этой теоремы воспользуемся формальным преобразованием двух строчек кванторов. Имеем:
f(x) непрерывна в x0 ∀ε>0,∃δ∀x|x−x0|<δ |f(x)−f(x0)|<ε ψ(e)непрерывна в t0 ∀δ>0∃η∀t |t−t0|<η|φ(t)−φ(t0)|<δ Выписывая кванторы, получим, что:
Непрерывность элементарных функций
-
f(x) = C, (где С – постоянная) непрерывна на R, т.к.
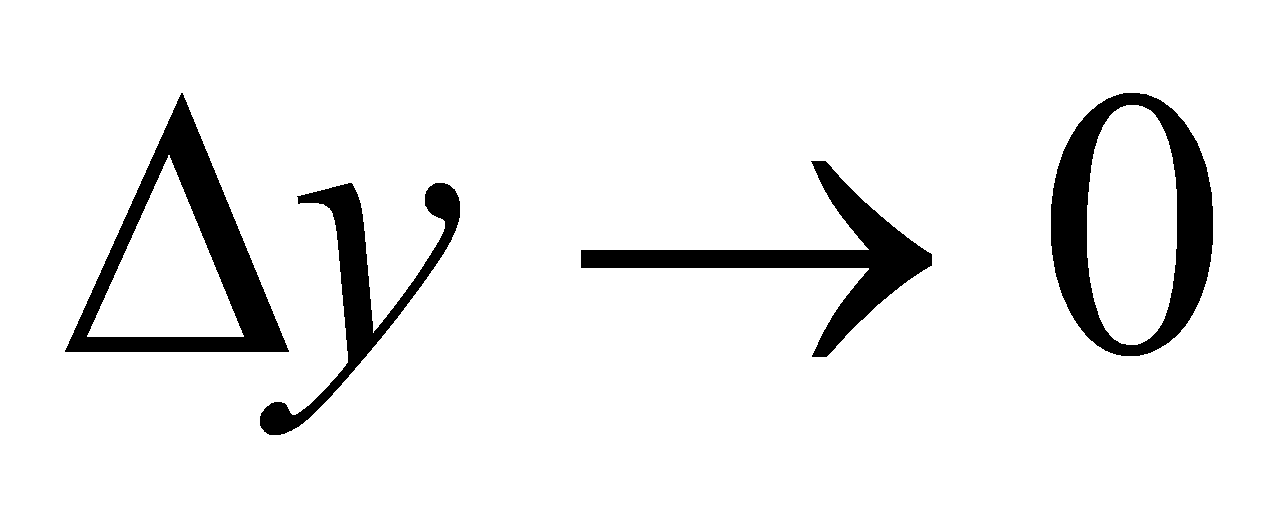 при любом x.
при любом x. -
f(x) = x, непрерывна на R, т.к.
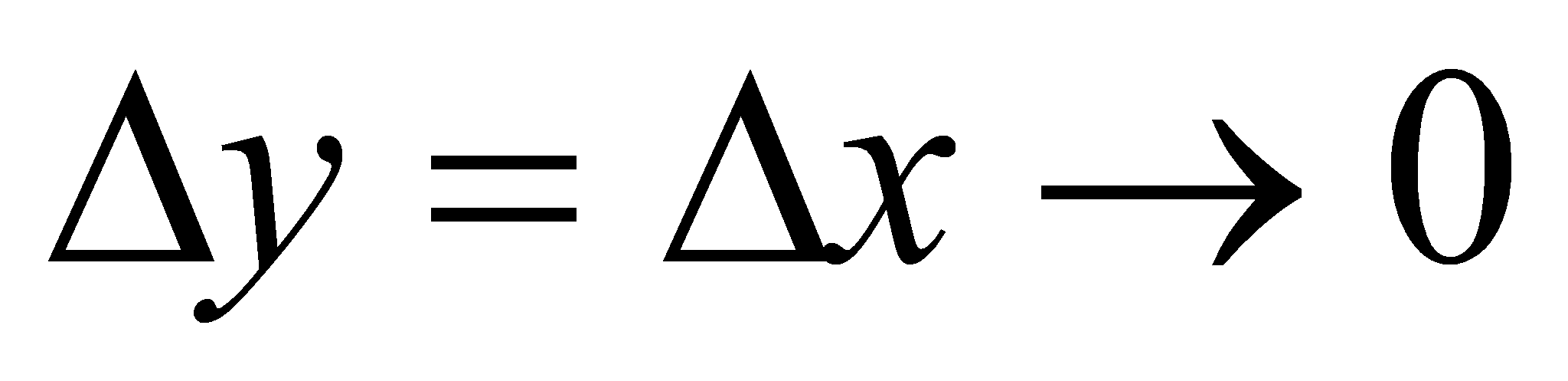 при
при 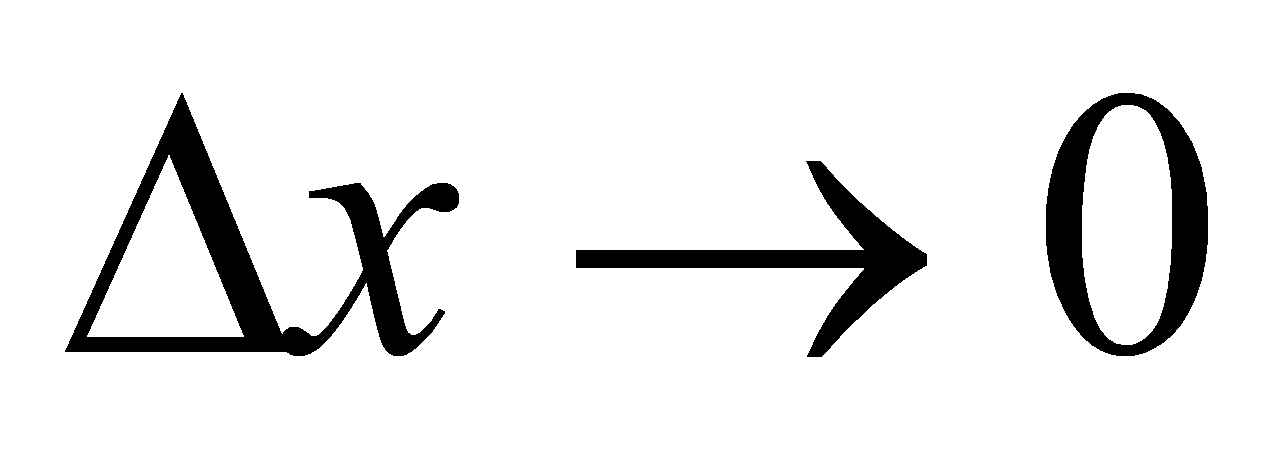 .
. -
f(x) =
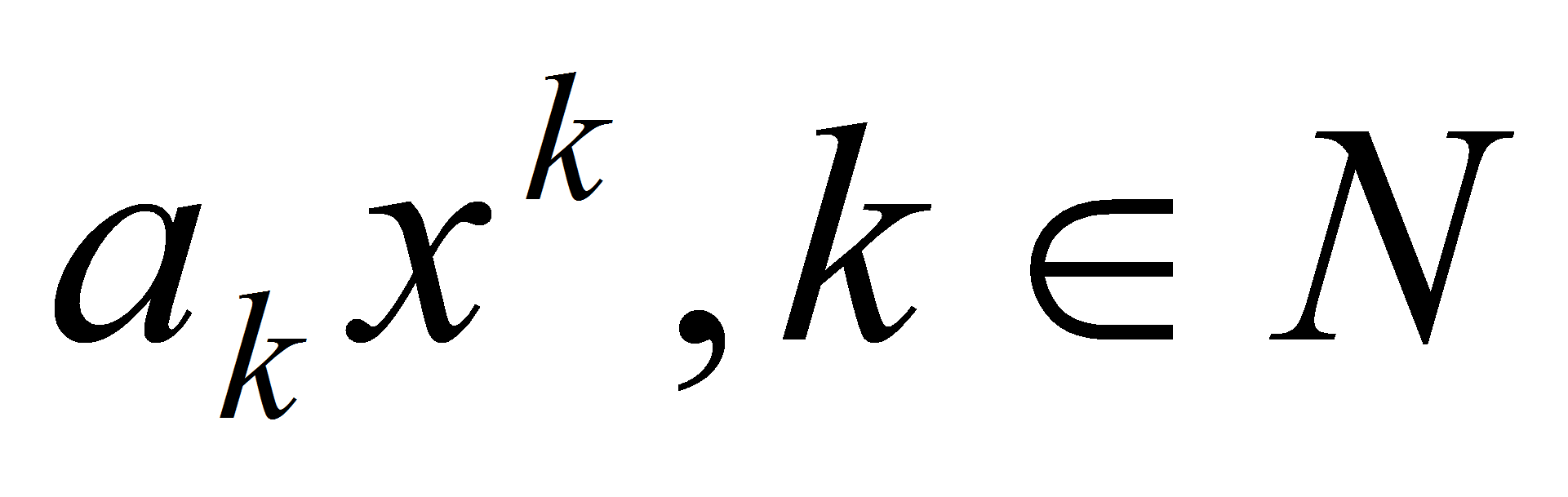 , непрерывна на R как произведение непрерывных функций.
, непрерывна на R как произведение непрерывных функций. -
f(x) =
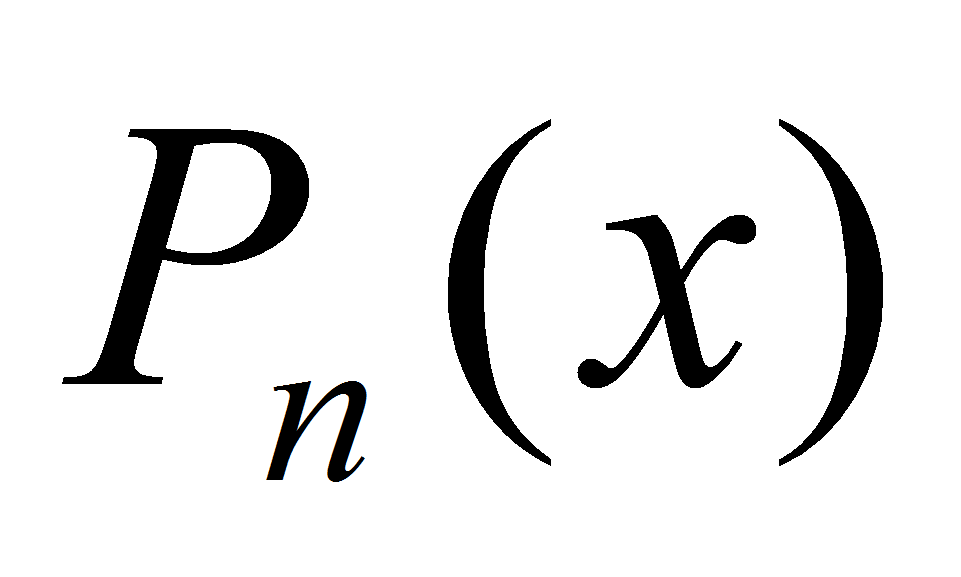 , непрерывна на R, т.к. многочлен
, непрерывна на R, т.к. многочлен 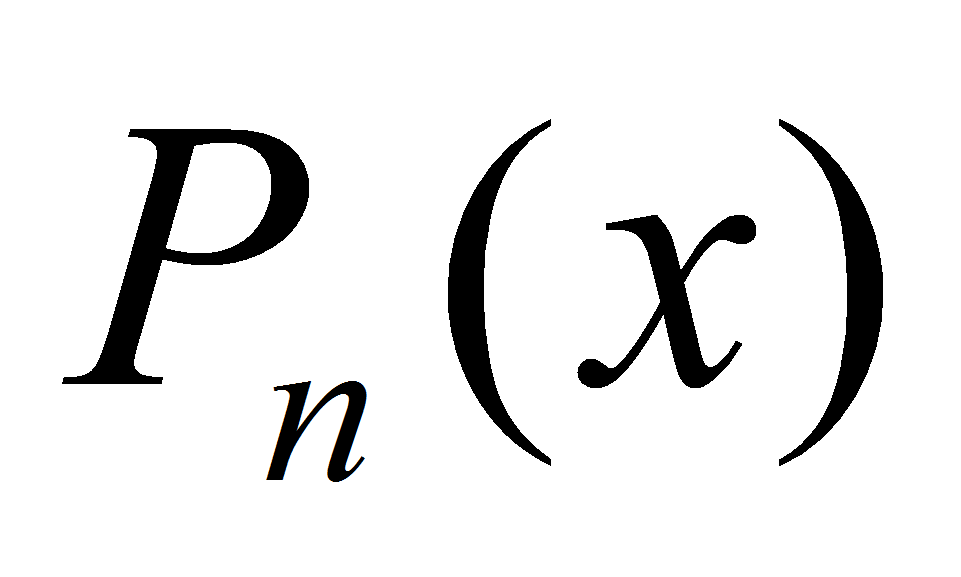 есть сумма непрерывных функций.
есть сумма непрерывных функций. -
f(x) =
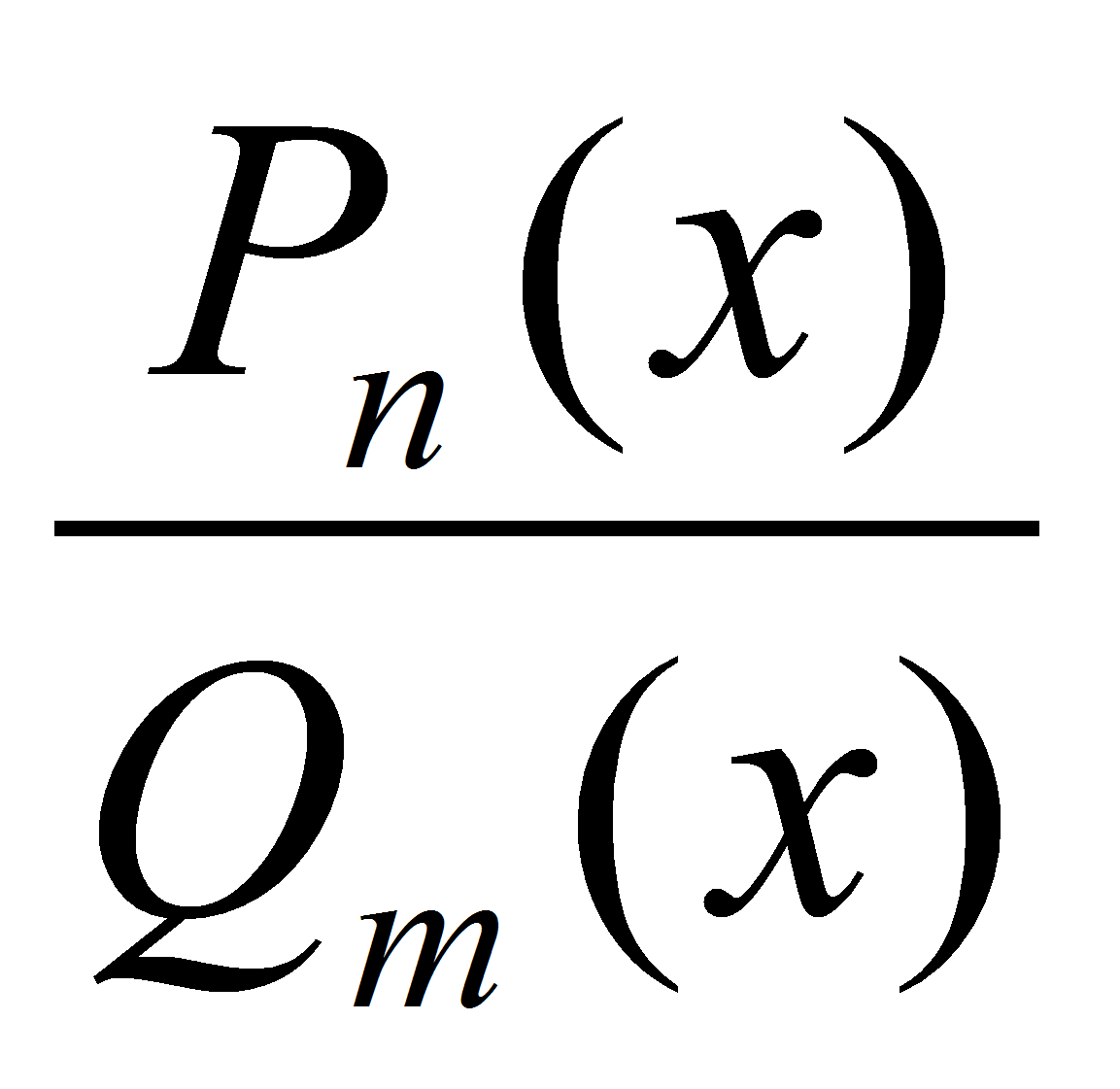 , где P и Q – многочлены степени n и m соответственно, непрерывна на R кроме тех x, при которых Q обращается в нуль, как частное непрерывных функций.
, где P и Q – многочлены степени n и m соответственно, непрерывна на R кроме тех x, при которых Q обращается в нуль, как частное непрерывных функций. -
f(x) = sin(x), f(x) = cos(x)
Пусть 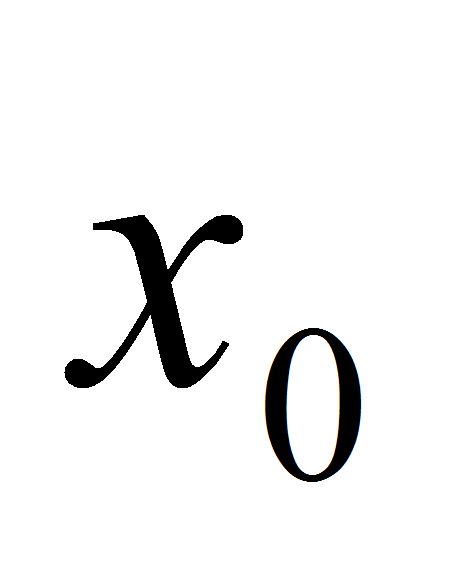 – произвольная точка множества R. Тогда sinx-sin
– произвольная точка множества R. Тогда sinx-sin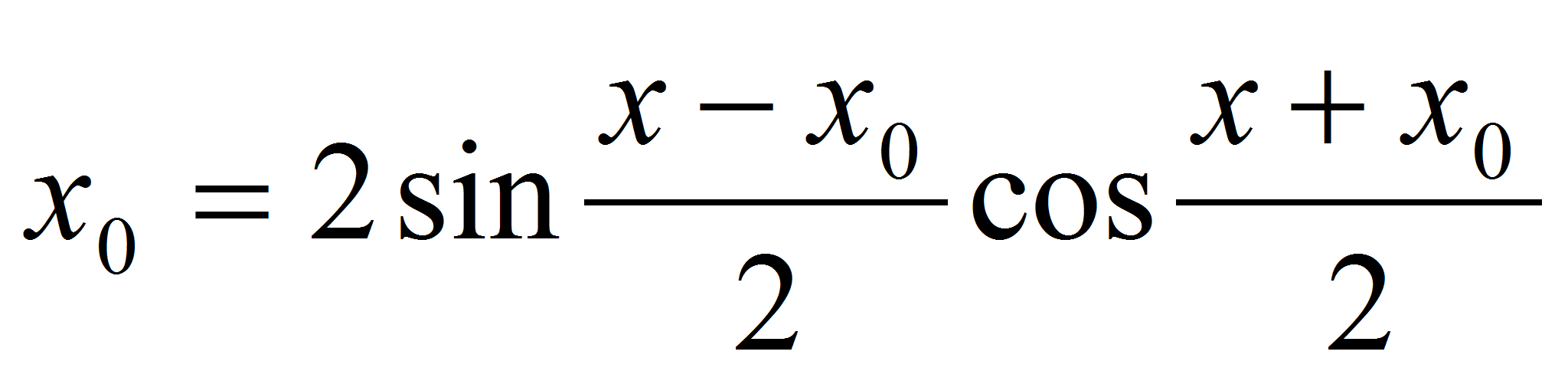 . Так как
. Так как 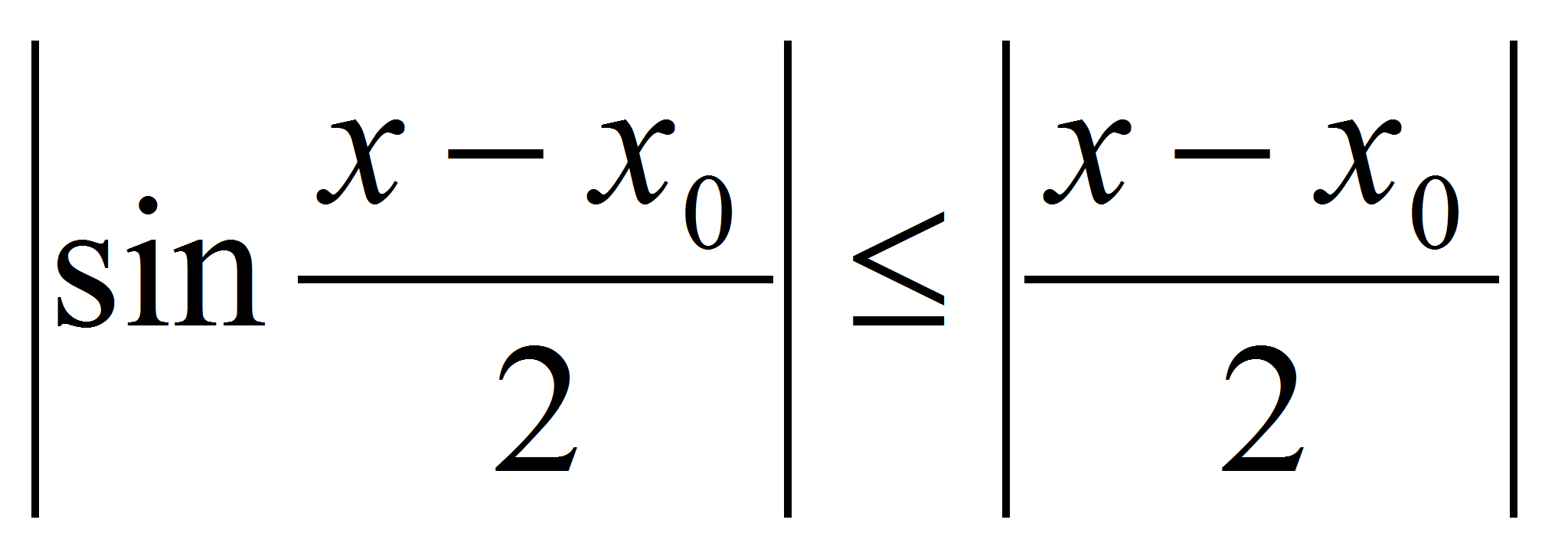 , а
, а 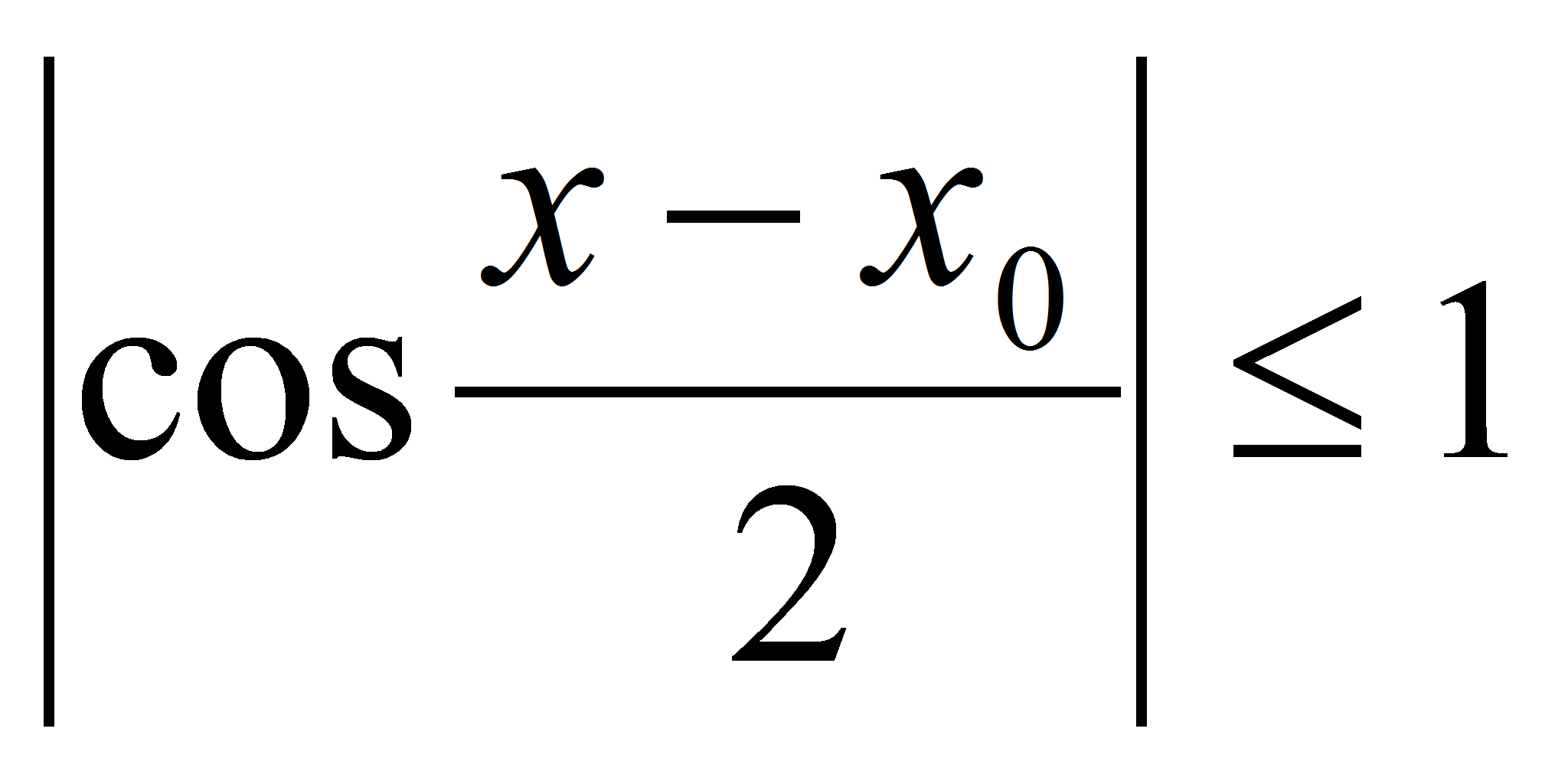 , то
, то 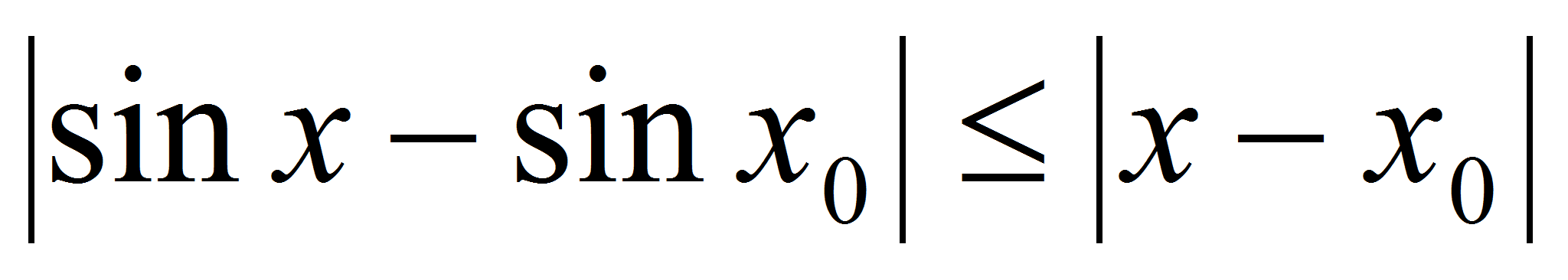 , откуда следует, что функция f(x) = sin(x) – непрерывна.
, откуда следует, что функция f(x) = sin(x) – непрерывна.
Аналогично рассуждая, можно доказать непрерывность косинуса. Из непрерывностей синуса и косинуса следуют непрерывности тангенса и котангенса, учитывая что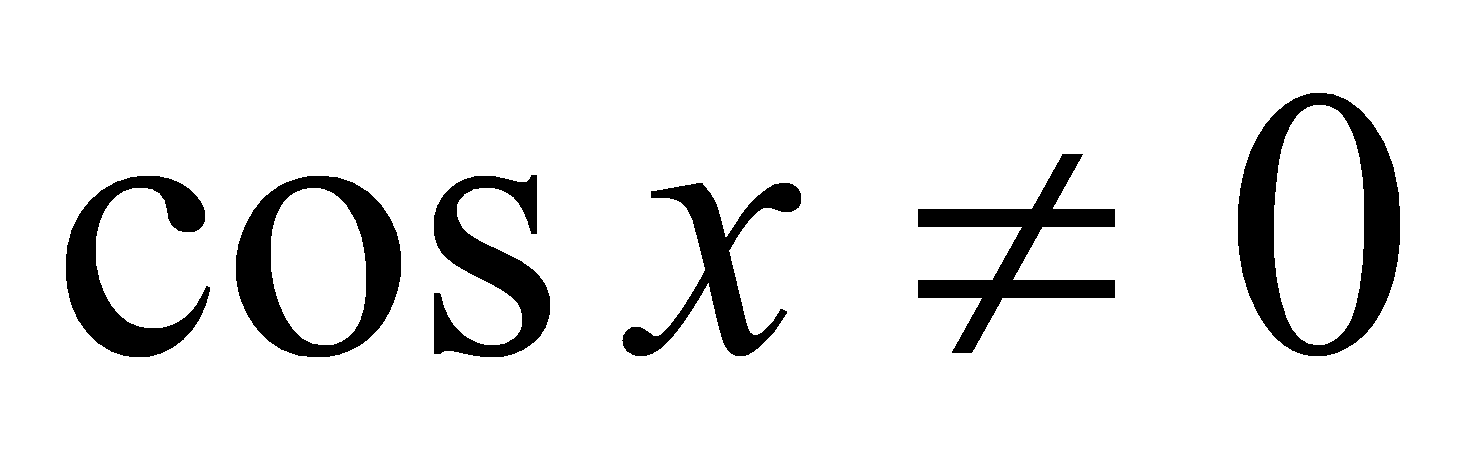 (для тангенса) и
(для тангенса) и 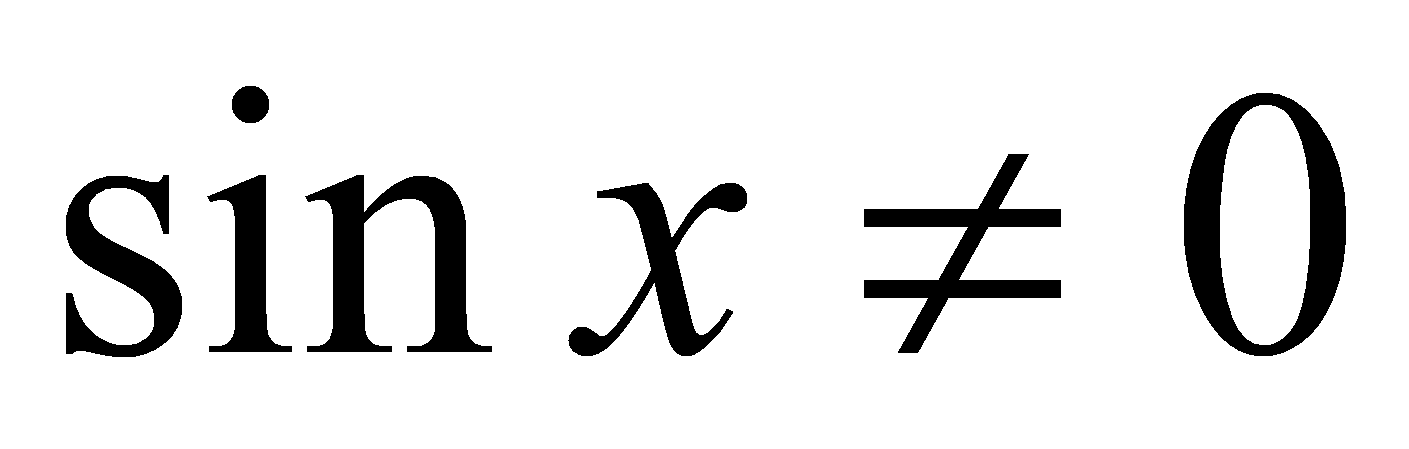 (для котангенса).
(для котангенса).
-
f(x) = arcsin(x), f(x) = arccos(x), f(x) = arctg(x), f(x) = arcctg(x) , непрерывны на своей области определения. Это следует из теоремы об обратной функции, примененной не ко всей тригонометрической функции (к примеру, sin(x)), а к ее отрезку (для sin(x) это отрезок
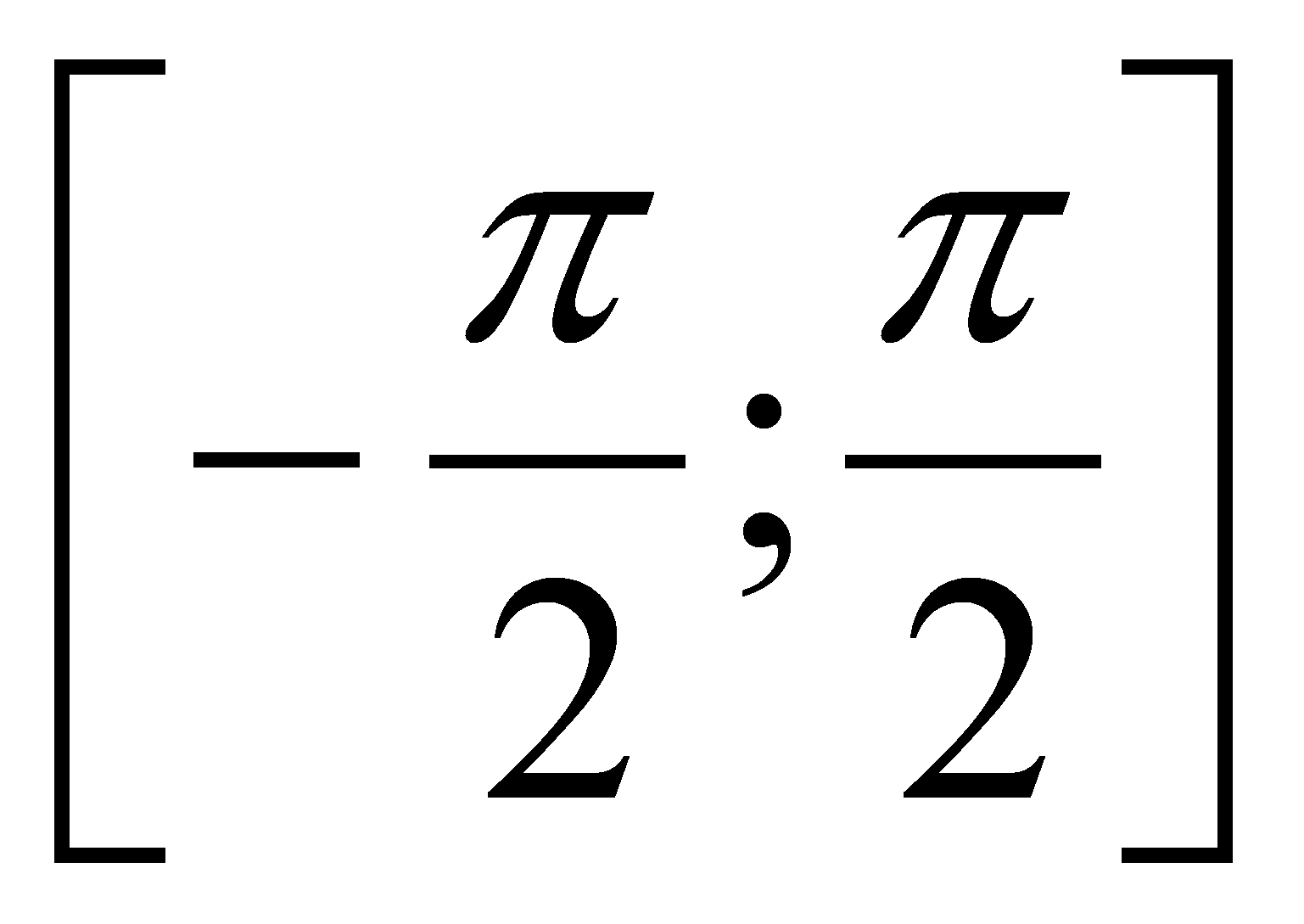 ).
). -
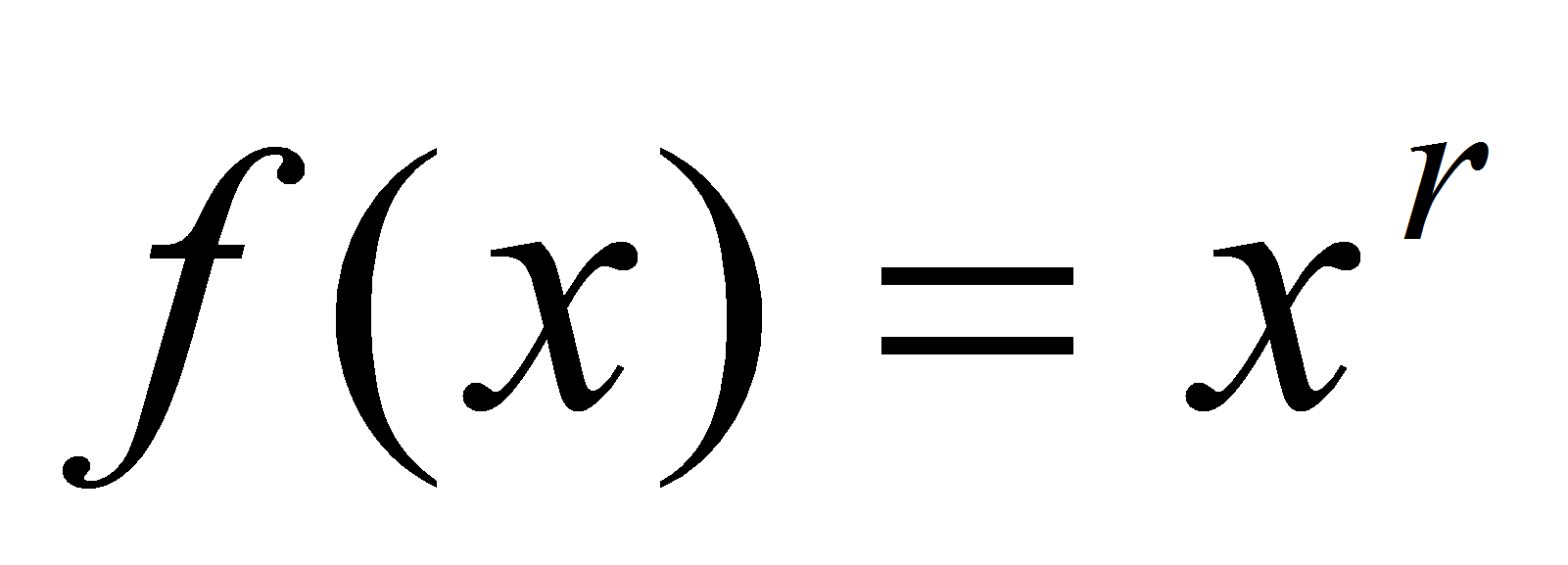 , где r – рациональное. Представим r = m / n,
, где r – рациональное. Представим r = m / n, 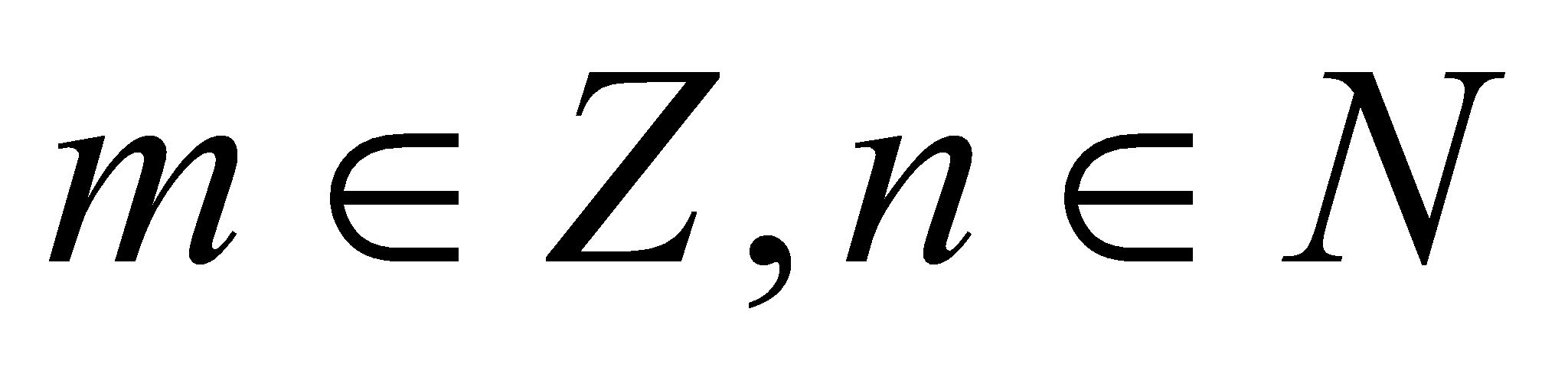 . Тогда
. Тогда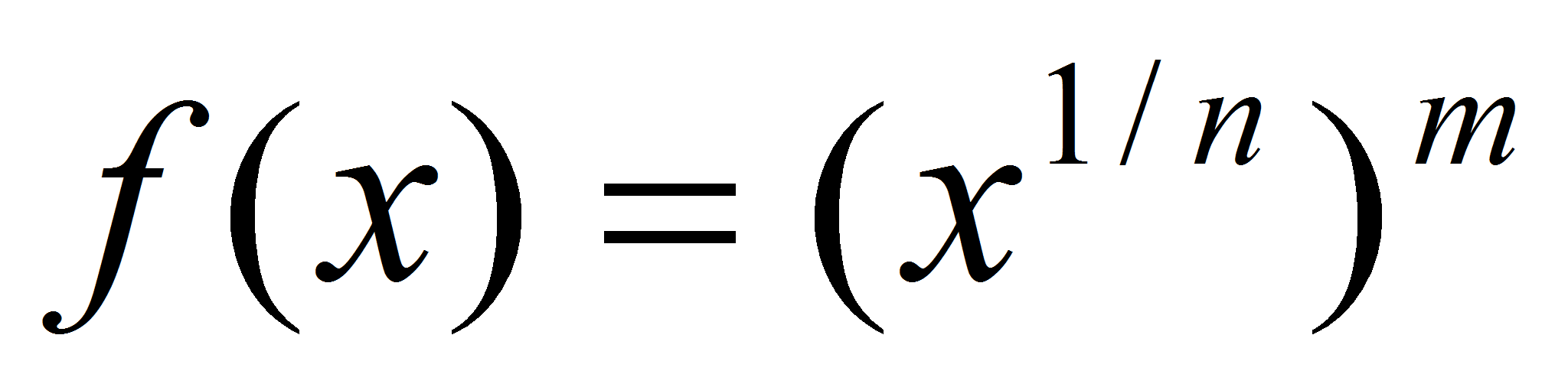 . Функция
. Функция 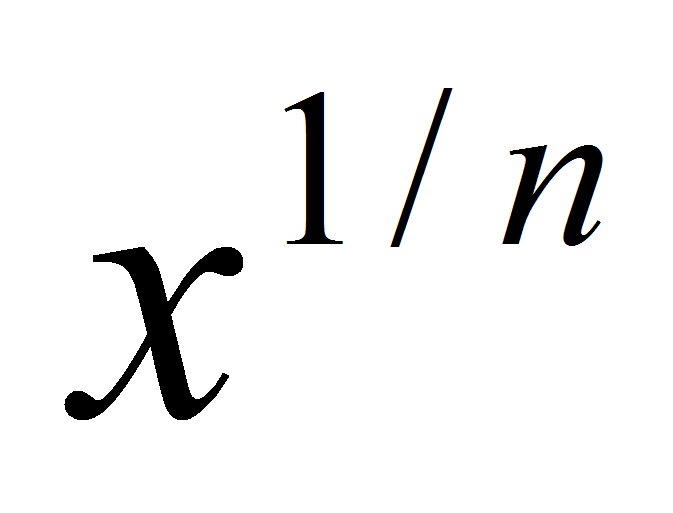 непрерывна и строго возрастает на R. По п. 2
непрерывна и строго возрастает на R. По п. 2 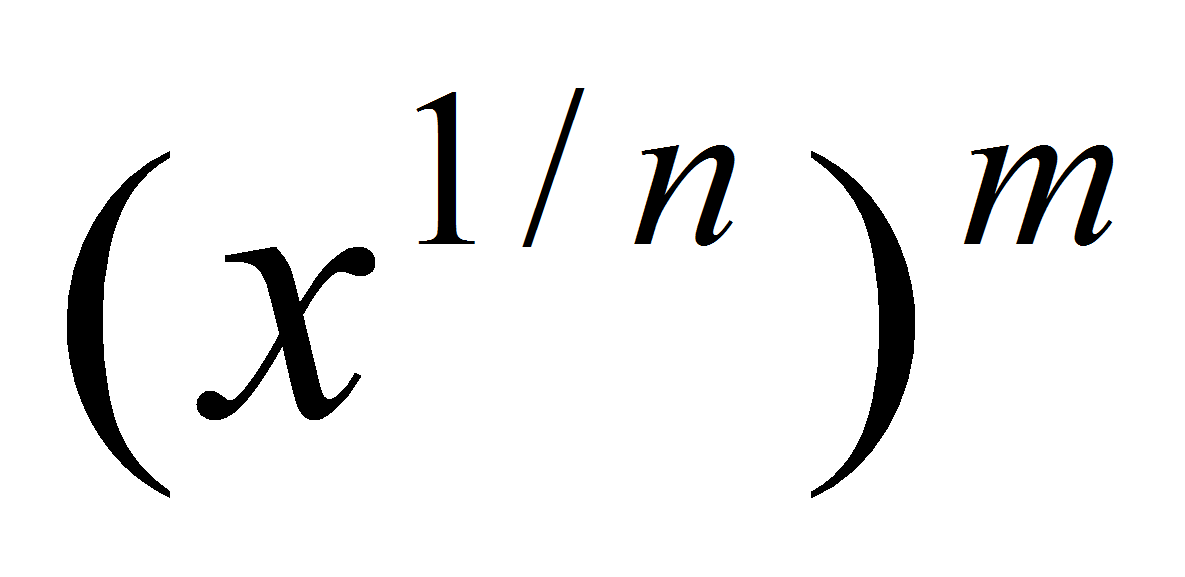 также непрерывна.
также непрерывна. -
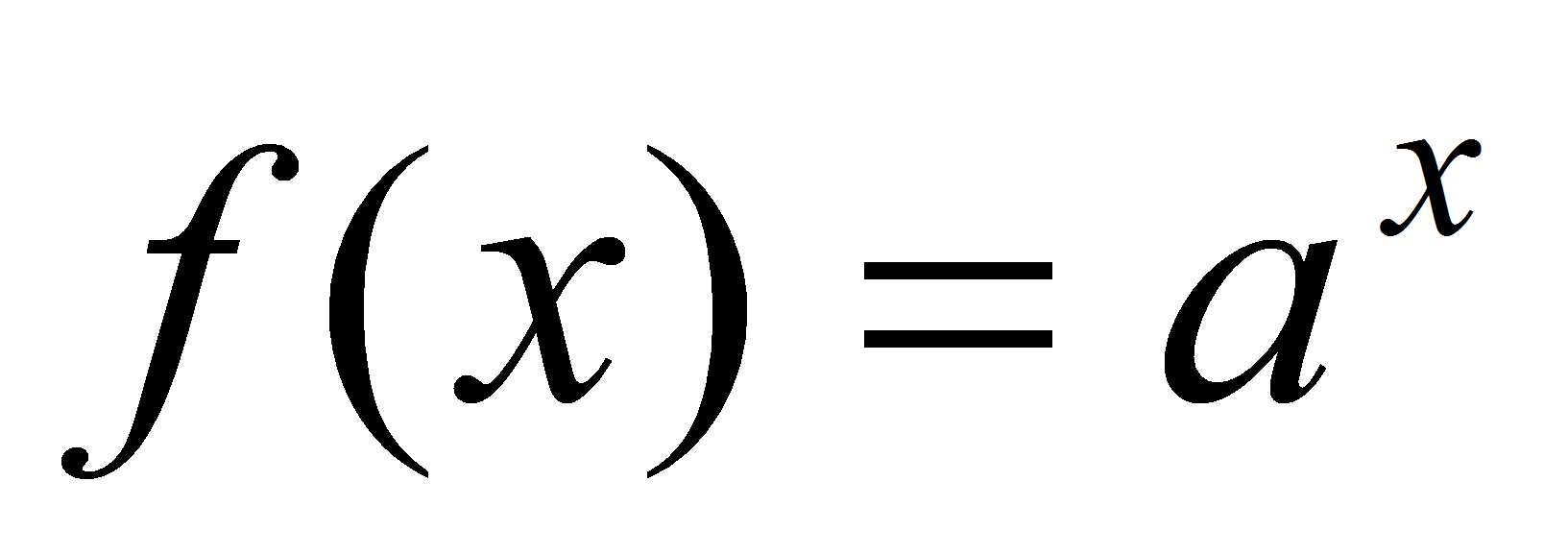 , a > 1, непрерывна на R. Пусть
, a > 1, непрерывна на R. Пусть 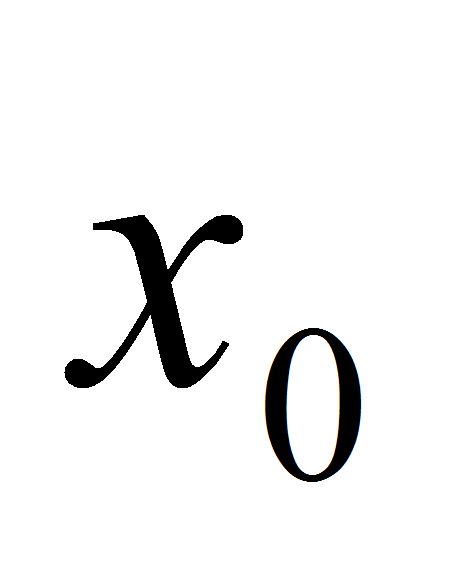 – произвольная точка множества R,
– произвольная точка множества R,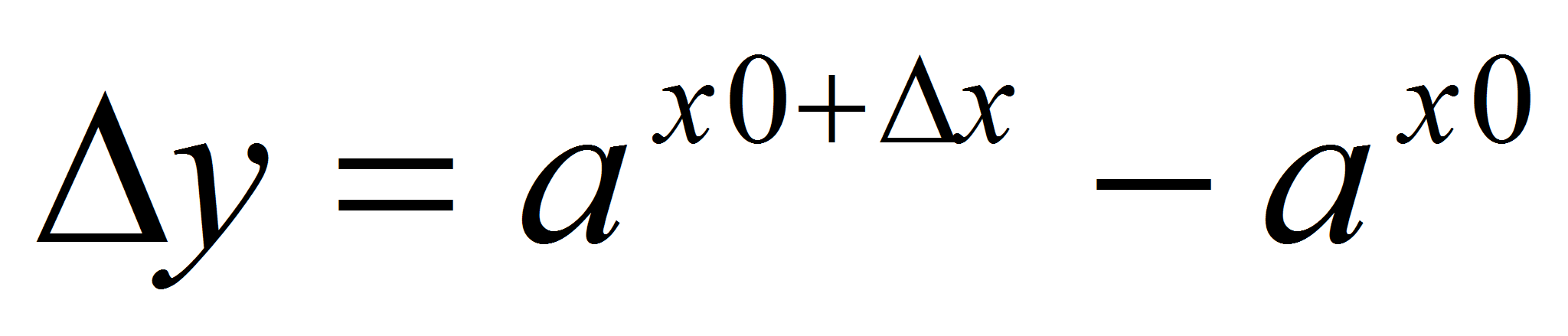 =
=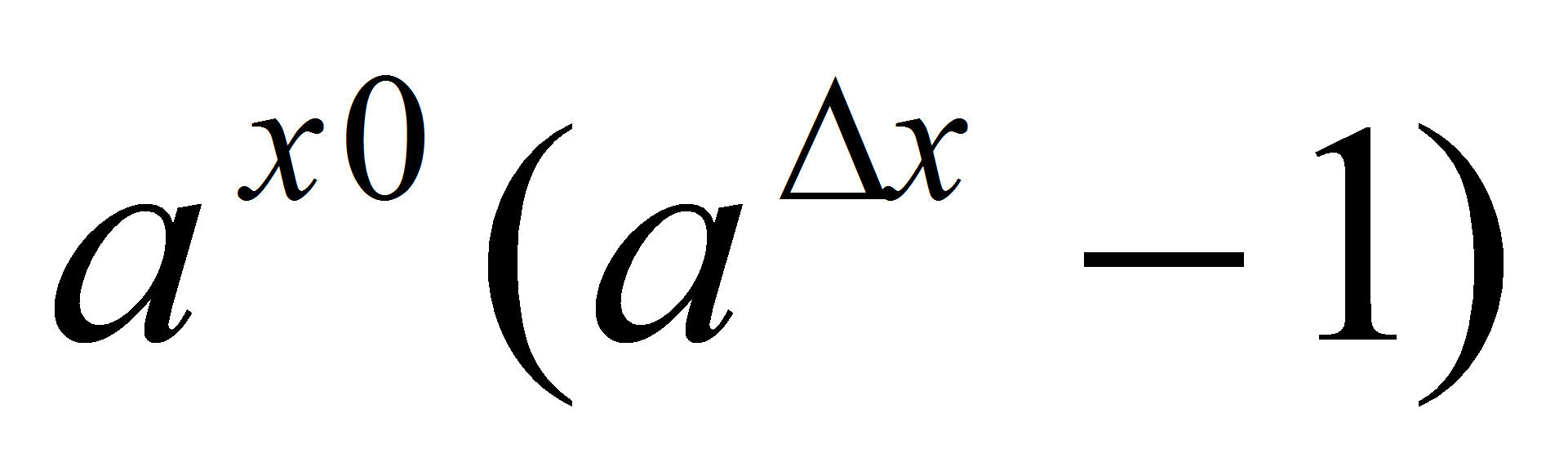 . Докажем, что
. Докажем, что 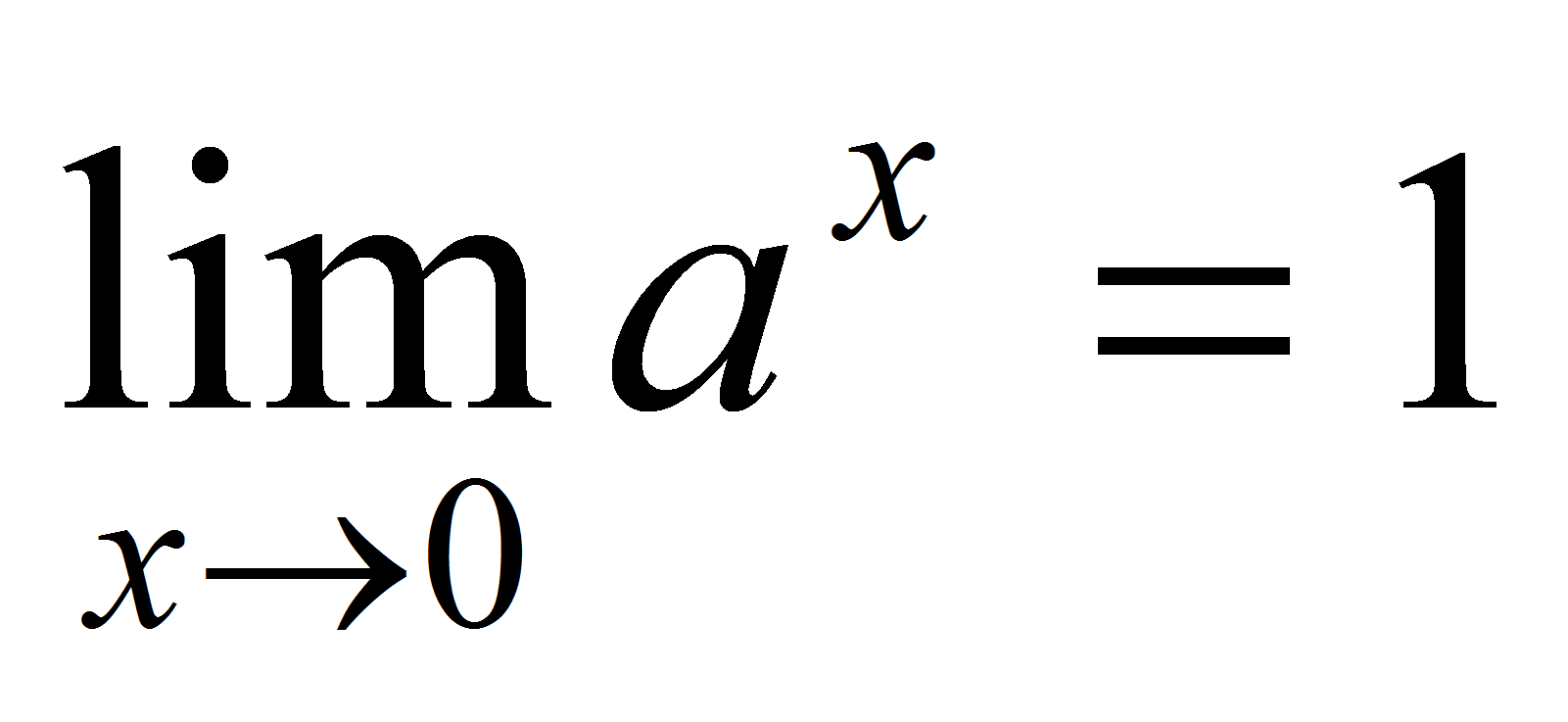 . Пусть
. Пусть 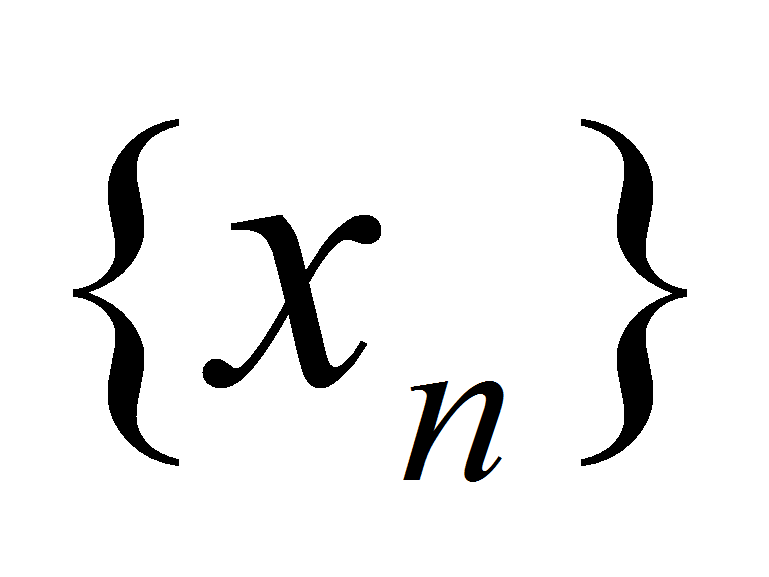 - произвольная последовательность вещественных чисел такая, что
- произвольная последовательность вещественных чисел такая, что 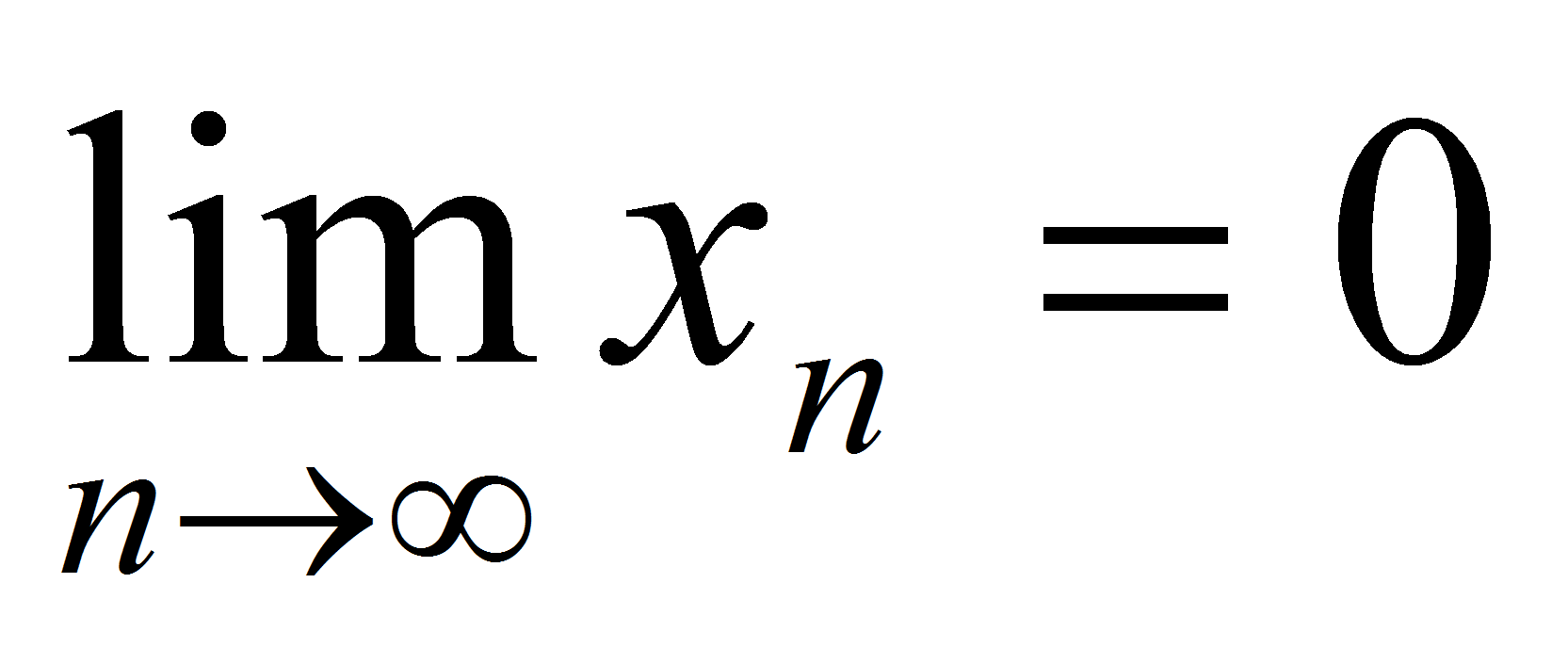 . В силу свойств вещественных чисел найдутся последовательности рациональных чисел
. В силу свойств вещественных чисел найдутся последовательности рациональных чисел 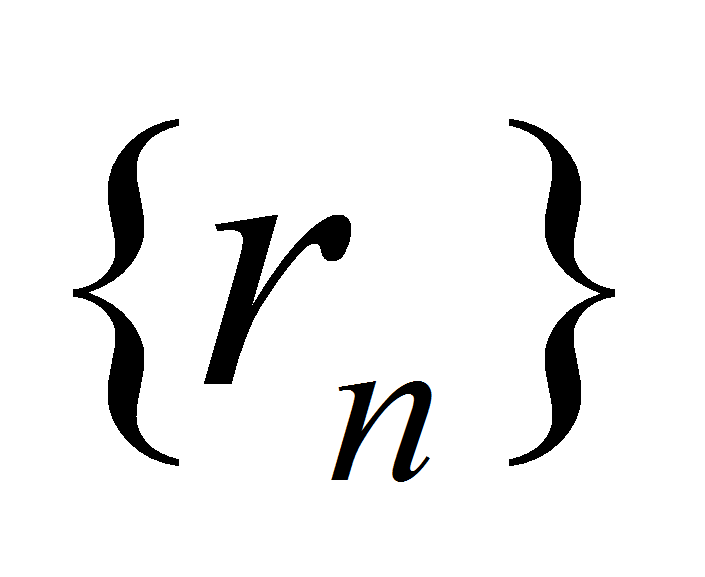 и
и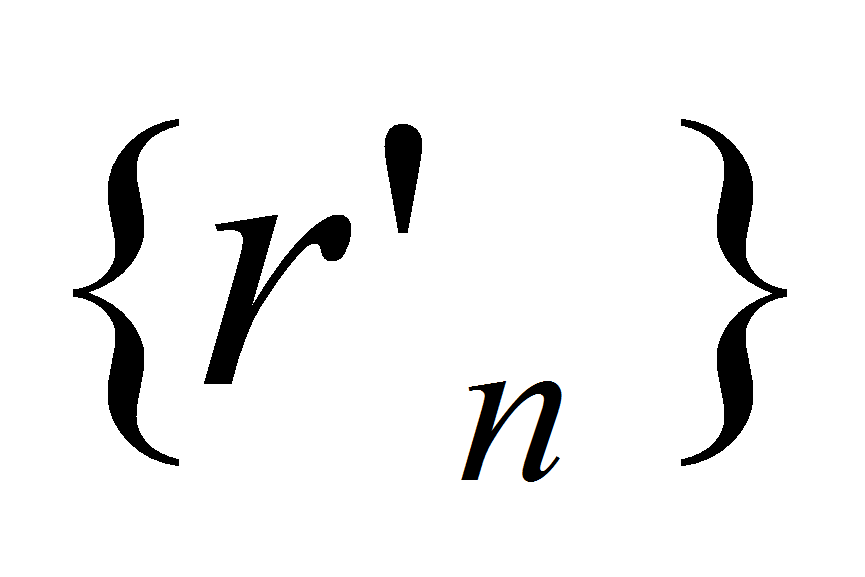 , удовлетворяющие при
, удовлетворяющие при 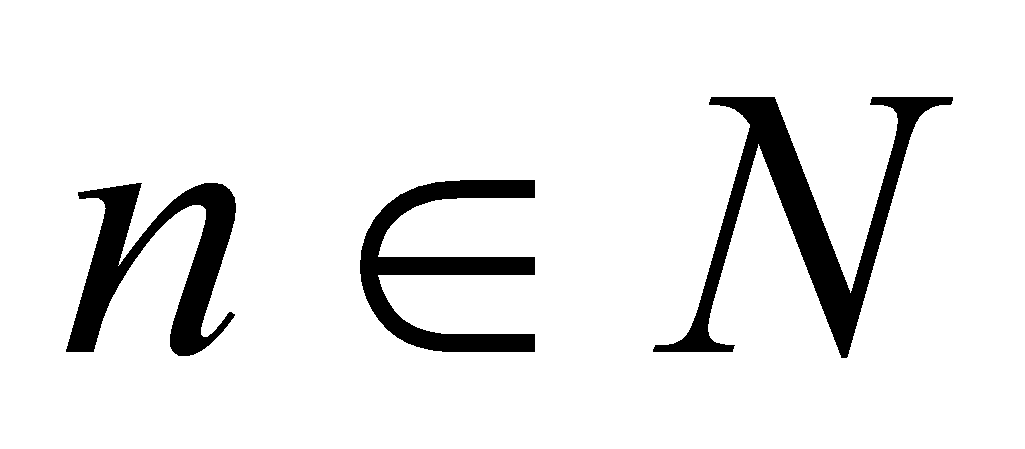 условию:
условию: 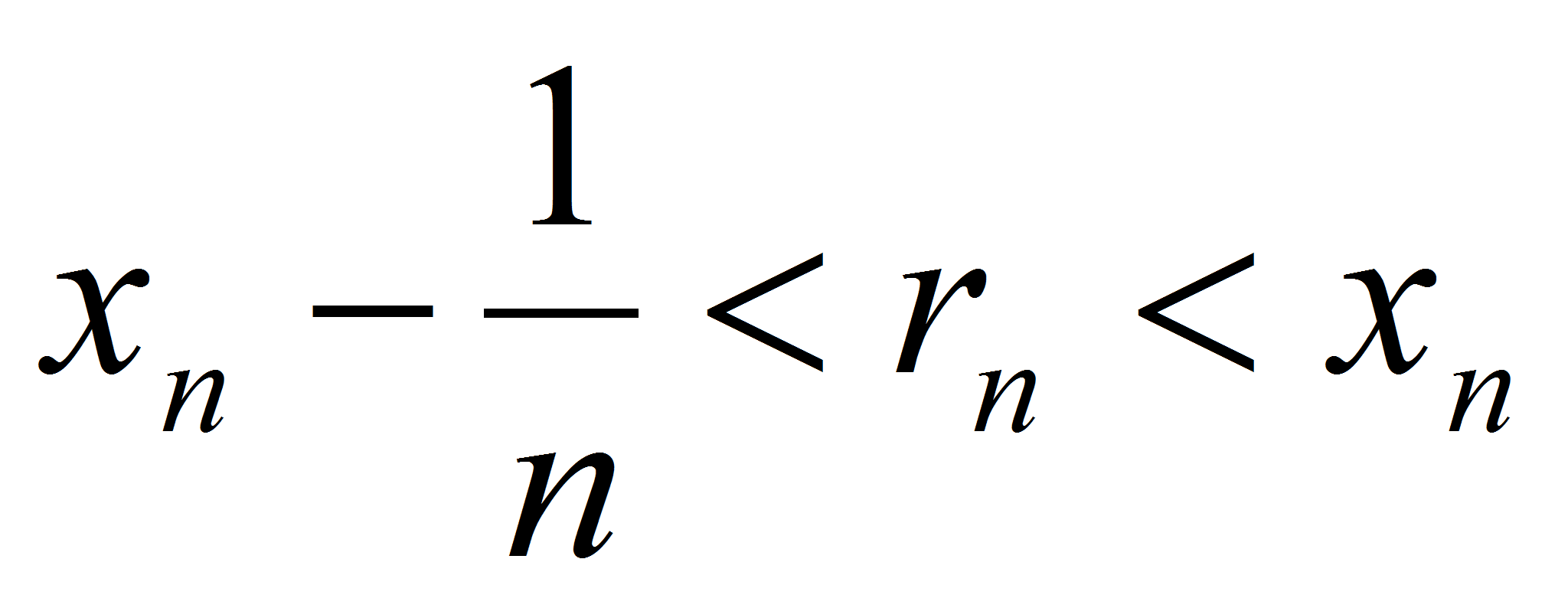 <
<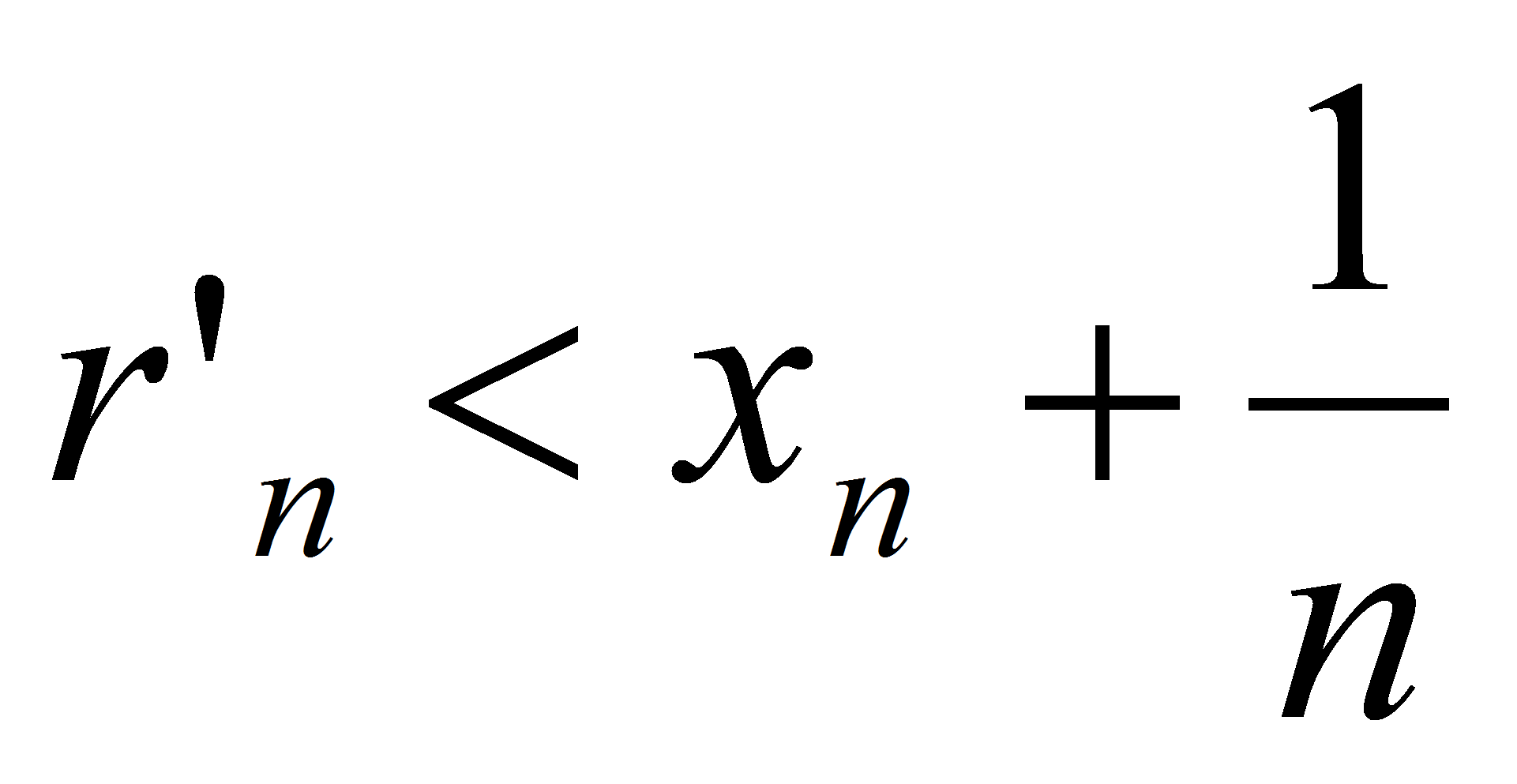 , откуда
, откуда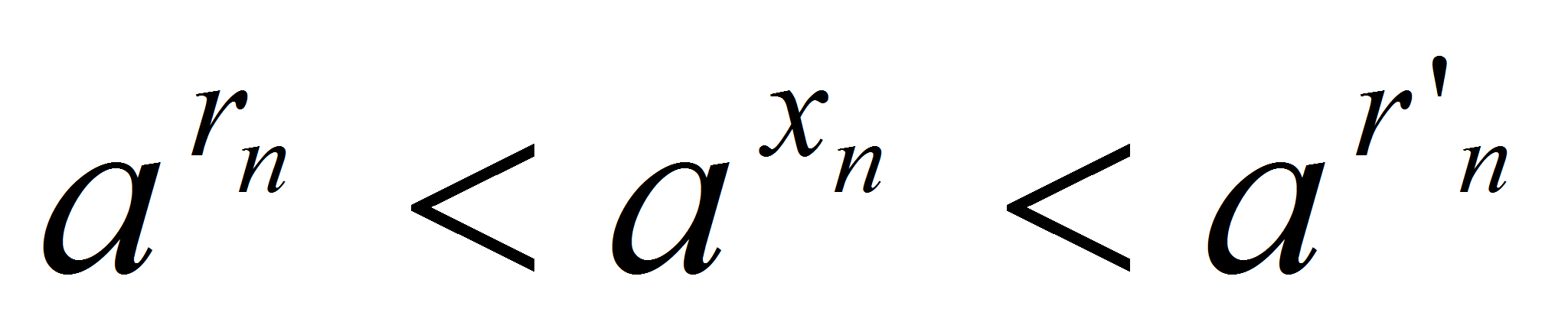 . Так как
. Так как 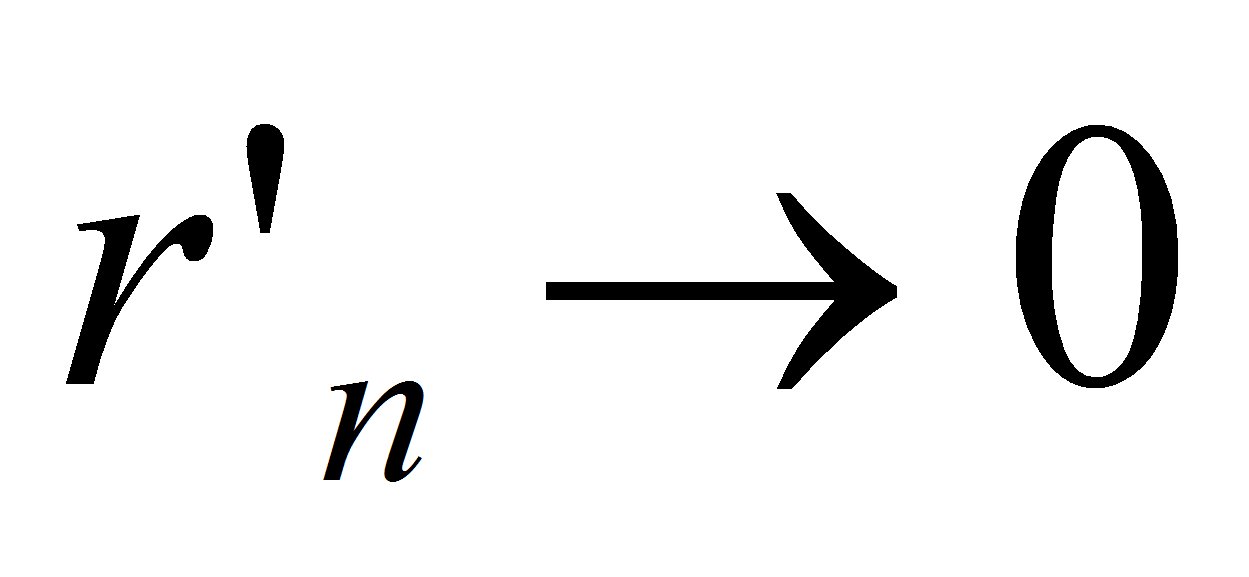 и
и  , то
, то 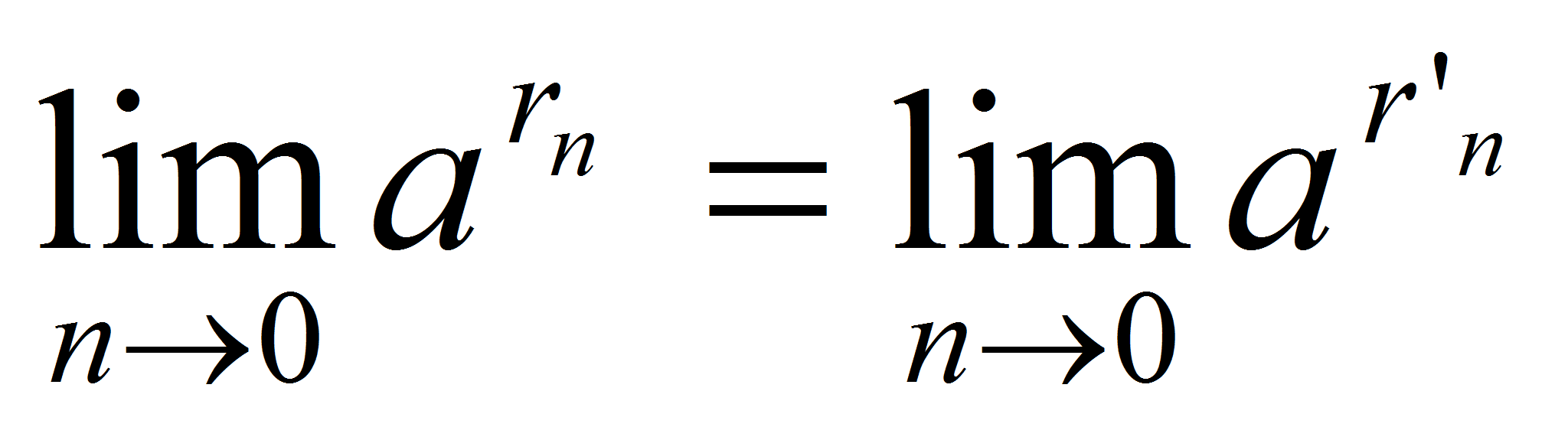 =1. Отсюда и
=1. Отсюда и 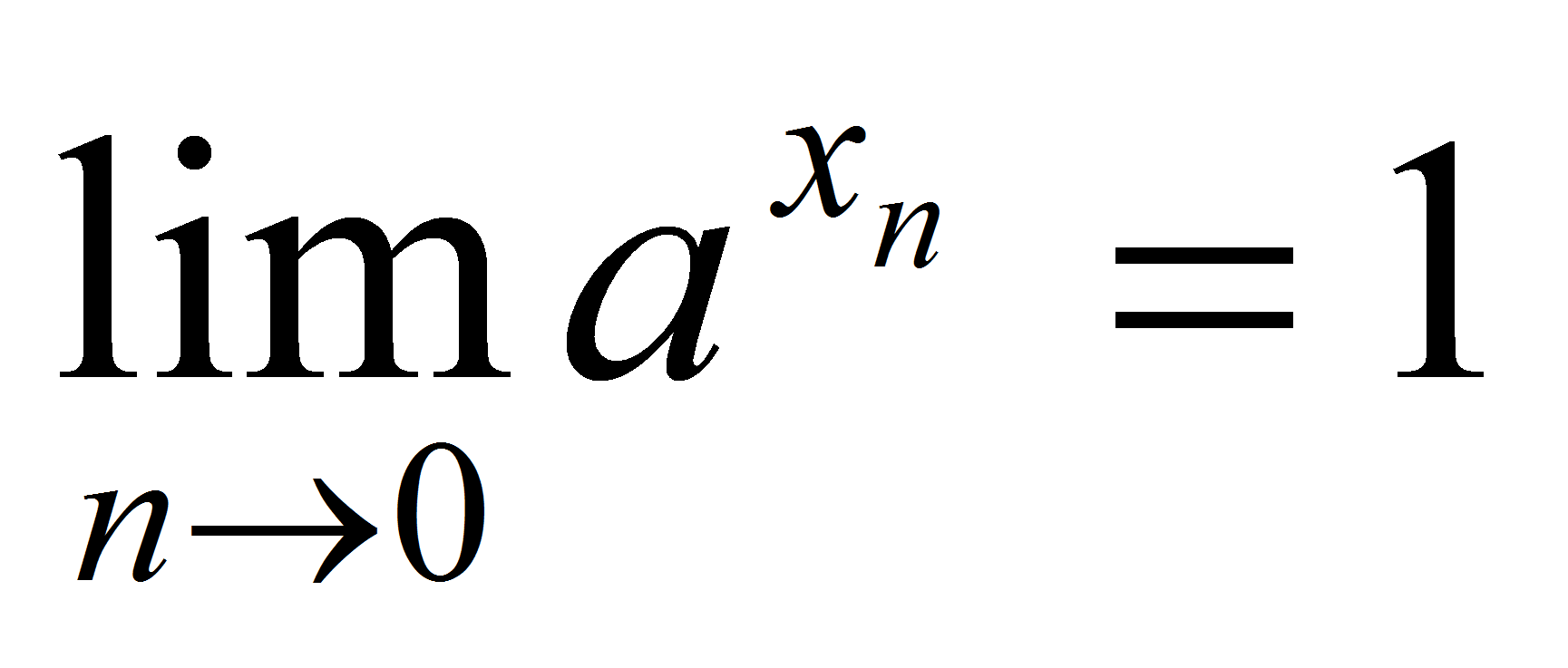 , ч.т.д.
, ч.т.д. -
Логарифмическая функция непрерывна, что следует из непрерывности показательной функции по теореме об обратной функции.

