Функция 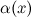 называется бесконечно малой при
называется бесконечно малой при 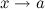 (или в точке
(или в точке 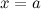 ), если
), если 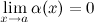
Подробная теория про бесконечно малые функции по ссылке.
 |
|
||||||
Вопрос 29. Сравнение б.м. Свойства.
Сравнение бесконечно малых функцийОпределение
Функция Подробная теория про бесконечно малые функции по ссылке. Пример
Функция
Бесконечно малые функции одного порядкаПусть Определение
Функции Пример
Рассмотрим функции
Найдем предел отношения этих функций при
Так как предел равен конечному, отличному от нуля числу, то рассматриваемые функции Бесконечно малые функции более низкого и высокого порядковОпределение
Если Пример
Функция
Определение
Если Пример
Рассмотрим функцию
А поэтому, функция Определение
Если Пример
Функция
Эквивалентные (равносильные) бесконечно малые функцииОпределение
Если Пример
Функции
а во-вторых:
Следствие: а) если б) если Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов. Пример. Найти предел Так как Если Тогда говорят, что
|
|||||||
|
|||||||