Граф является деревом, если он удовлетворяет следующей теореме.
Теорема. Для графа G= <X,U> следующие утверждения эквивалентны:
1) G - дерево;
2) любые две вершины в графе G соединены единственной простой цепью;
3) граф G связен и имеет |X| - 1 ребер;
4) граф G не содержит циклов и имеет |X| - 1 ребер;
5) граф G не содержит циклов, но добавление ребра между любыми двумя несмежными вершинами приводит к появлению одного цикла;
6) граф G связен, но утрачивает это свойство после удаления любого ребра.
Теорема Кэли о числе деревьев — названное в честь А. Кэли явное выражение в теории графов для числа деревьев с данным числом пронумерованных вершин. А именно, оказывается, что на n вершинах, пронумерованных числами от 1 до n, существует ровно 
различных деревьев.
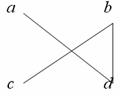
Граф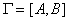 
называется планарным, если хотя бы одна из его геометрических интерпретаций такова, что ребра графа пересекаются только в его вершинах. Например, граф:
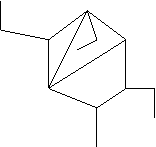
Пусть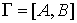 
- плоский граф. Это означает, что имеется определенное изображение его на плоскости, в котором ребра пересекаются только в вершинах. Каждый простой цикл такого графа ограничивает две части плоскости: одна - внутренняя (ограниченная), другая - внешняя (неограниченная):
Теорема (Л. Эйлер, 1736 г.)
Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.
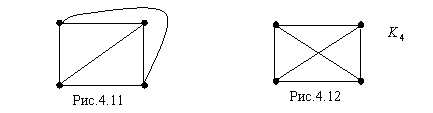
На 4.11 плоский граф, на 4.12 неплоский.
